Question

Знайдіть для функції f(x)=2x2 -7 таку первісну, графік якої проходить через точку (0;2).

Answer 1

$\displaystyle\bf\\f(x)=2x^{2} -7$

Общий вид первообразных для этой функции имеет вид :

$\displaystyle\bf\\F(x)=2\cdot\frac{x^{3} }{3} -7x+C=\frac{2}{3} x^{3} -7x+C$

График этой первообразной проходит через точку с координатами :

(0 ; 2) , то есть  x = 0 , F(x) = 2 . Найдём чему равно значение C :

$\displaystyle\bf\\2=\frac{2}{3} \cdot 0^{3}-7\cdot 0+C \\\\2=0-0+C\\\\C=2\\\\Otvet \ : \ \boxed{F(x)=\frac{2}{3} x^{3} -7x+2}$

Answer 2

Для функций f(x)=2x^2-7 и f(x)=2x2-7 найти такие первообразные, графики которых проходят через точку (0;2).

Ответ:

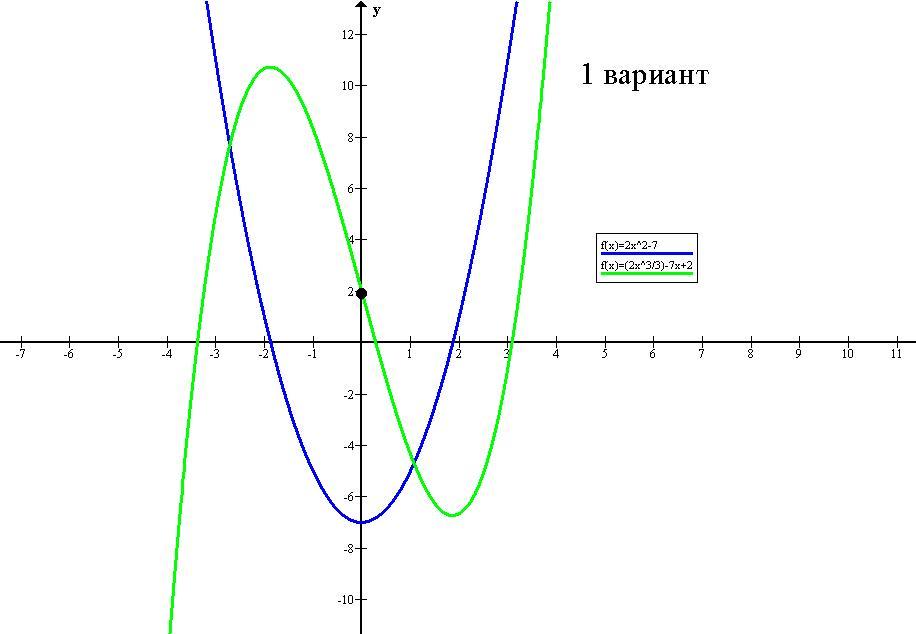
1) Первообразная функции f(x)=2x^2-7, которая проходит через точку (0;2), имеет вид F(x)=(2x³/3)-7x+2.

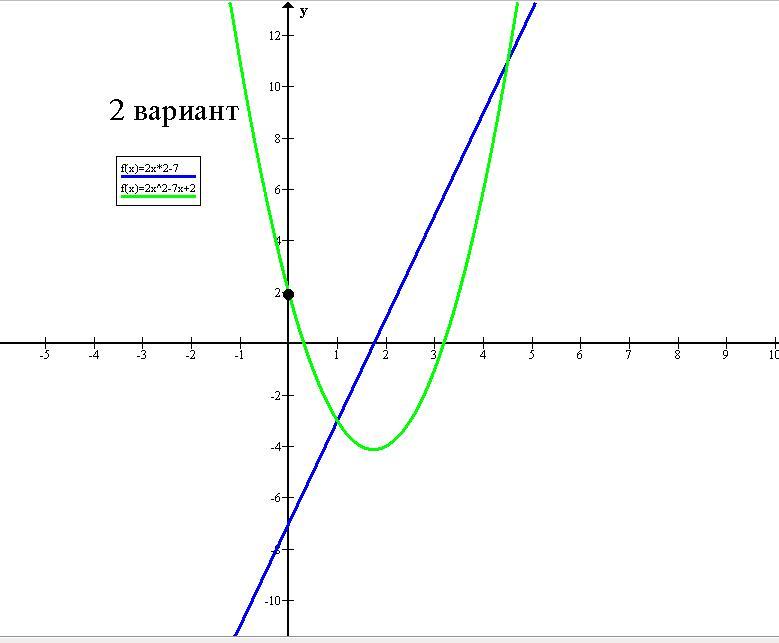
2) Первообразная функции f(x)=2x*2-7, которая проходит через точку (0;2), имеет вид F(x)=2x²-7x+2.

Объяснение:

Так как двойка после переменной - скорее всего показатель степени, предлагаю рассмотреть два случая: в первом функция имеет вид f(x)=2x^2-7, во втором - f(x)=2x*2-7.

1 вариант. f(x)=2x^2-7.

Для начала найдём общий вид первообразных F(x) для функции f(x)=2x^2-7. Для этого берём неопределённый интеграл и используем правила интегрирования:

$\displaystyle {}F(x)=\int f(x)\ dx= \int(2x^2-7)\ dx = \int2x^2\ dx - \int7\ dx = \\\\=2\cdot\frac{x^{2+1}}{2+1} -7x+C=\frac{2x^3}{3}-7x+C$

Теперь для функции F(x)=(2x³/3)-7x+C находим такое значение константы С, при котором график ф-ции будет проходить через точку (0;2). Для этого в функцию поставляем х=0 и F(x)=2.

(2*0³)/3-7*0+C=2

0/3-0+C=2

C=2

Мы нашли значение константы С, при котором график функции F(x)=(2x³/3)-7x+C проходит через точку (0;2). Соответственно, первообразная функции f(x)=2x^2-7, которая проходит через точку (0;2), имеет вид F(x)=(2x³/3)-7x+2.

2 вариант. f(x)=2x*2-7.

Аналогично первому случаю, сначала находим общий вид первообразных для этой функции. Для этого используем неопределённый интеграл и правила интегрирования:

$\displaystyle {} F(x)=\int f(x)\ dx=\int(2x*2-7)\ dx =\int4x\ dx - \int7\ dx =\\\\= 4\cdot\frac{(x^{1+1})}{1+1} - 7x+ C =\not4 \cdot\frac{x^2}{\not2} - 7x + C=2x^2-7x+C$

Опять же, аналогично первому случаю, теперь находим такое значение константы С, при котором график функции будет проходить через точку (0;2).

2*0²-7*0+С=2

0-0+С=2

С=2

Значение константы С, при котором график функции F(x)=2x²-7x+C проходит через точку (0;2) равно двум. Первообразная функции f(x)=2x*2-7, которая проходит через точку (0;2), имеет вид F(x)=2x²-7x+2.