Предмет: Математика,
автор: spxxx124
Поясніть як обчислити даний вираз.
Приложения:
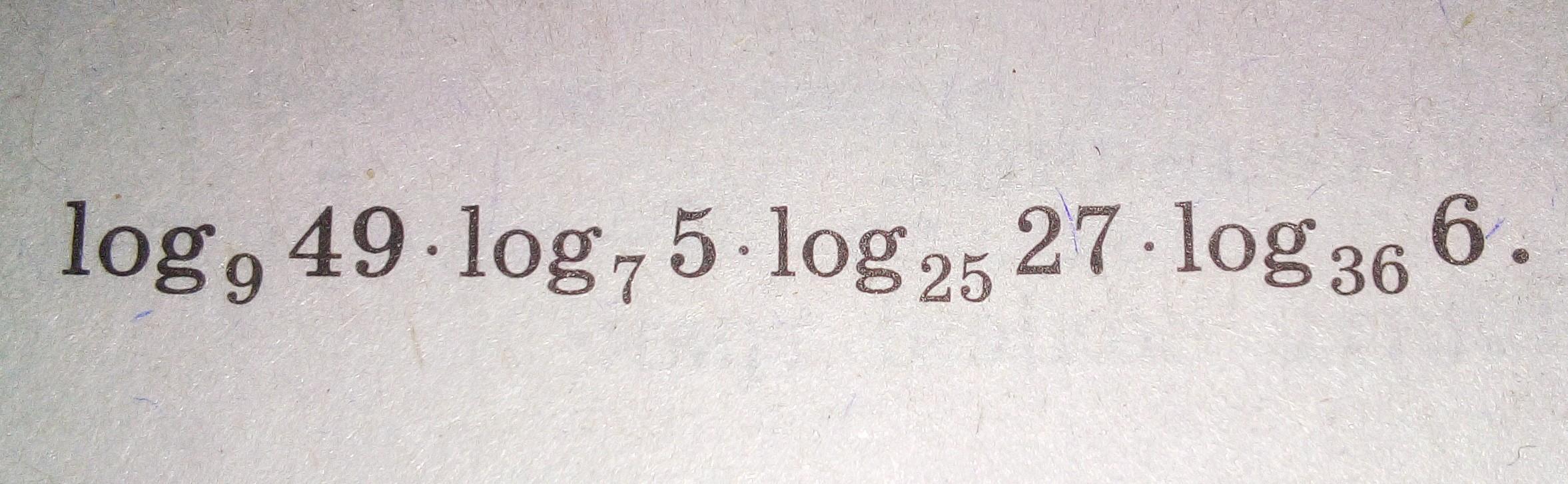
Ответы
Автор ответа:
2
Ответ: 0,75
Пошаговое объяснение:
Вспомним что
Тогда
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 5Sorry5
Предмет: Английский язык,
автор: richerd277
Предмет: Физика,
автор: aarhirenko50com