Предмет: Алгебра,
автор: bugubaevahmet4
помогите решить с объяснением
Приложения:
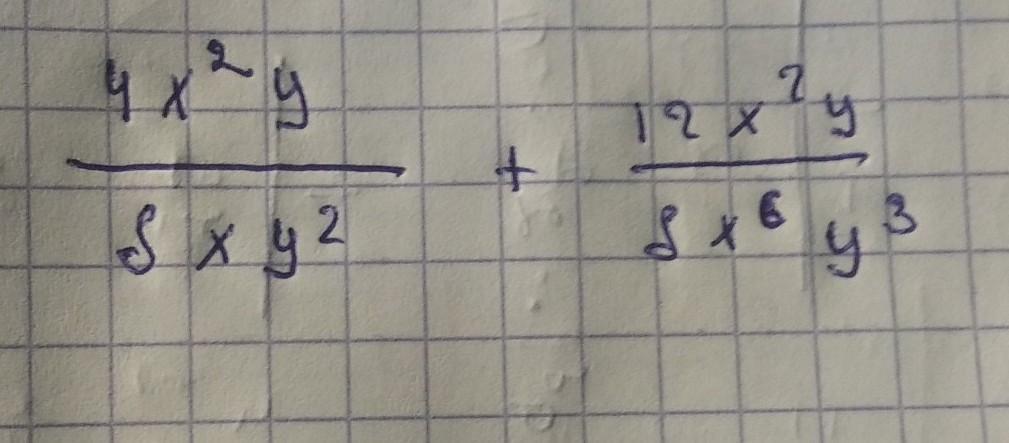
Ответы
Автор ответа:
2
Ответ:
Чтобы выделить общие множители в числителях и знаменателях
дробей, чтобы потом сократить дроби, пользуемся свойством
степеней .
Автор ответа:
0
Відповідь:
Пояснення:
Воспользуемся свойством степеней и еще помня что
Вспомним еще одно свойство степеней
Тогда получим
Похожие вопросы
Предмет: Русский язык,
автор: котик688
Предмет: Русский язык,
автор: майами1
Предмет: Русский язык,
автор: про100Лина1
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: staskostelianu