Предмет: Алгебра,
автор: JopenLaRe
Найти количество корней уравнения на отрезке
Приложения:
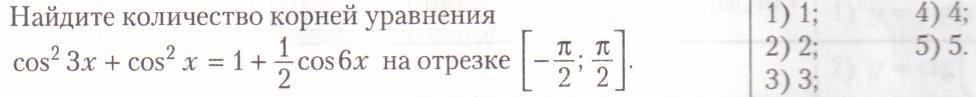
Ответы
Автор ответа:
2
Ответ:
2) 2
Объяснение:
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Приложения:
Автор ответа:
2
Ответ:
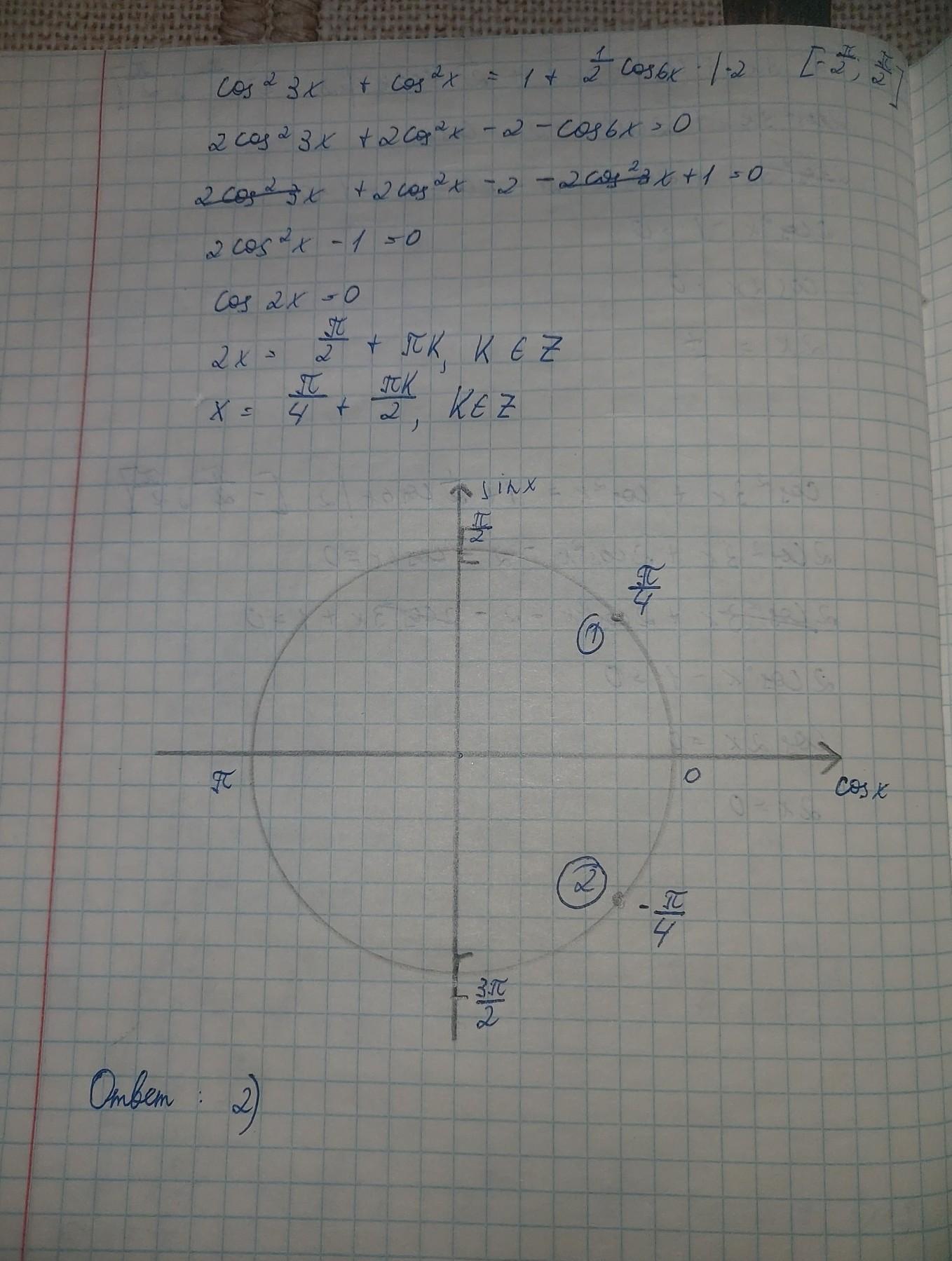
Уравнение на отрезке [ -π/2 ; π/2 ] имеет два корня
x₁ = -π/4
x₂ = π/4
Объяснение:
Найдите количество корней уравнения
cos² 3x + cos² x = 1 + 1/2 · cos6x на отрезке [ -π/2 ; π/2 ]
Воспользуемся формулой понижения степени
Подставим в исходное уравнение
Находим корни принадлежащие отрезку
При n = -2
При n = -1
При n = 0
При n = 1
Выходит , что на данном отрезке уравнение имеет два корня
Похожие вопросы
Предмет: Русский язык,
автор: marina9061
Предмет: Русский язык,
автор: Ли236
Предмет: Английский язык,
автор: TheCheevo
Предмет: Математика,
автор: katyakatya1990p0uyed
Предмет: География,
автор: ulabushmeleva874