Предмет: Математика,
автор: yatya
Решите систему пожалуйста
Приложения:
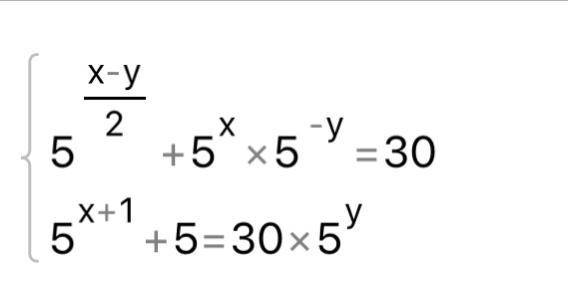
Ответы
Автор ответа:
4
Ответ:
Введём обозначения: .
Тогда . Систему перепишем в виде:
Решим первое уравнение системы .
, причём
.
Получили квадратное уравнение относительно дроби u/v . По теореме Виета легко подобрать корни этого уравнения:
Отрицательный корень не подходит.
Решим второе уравнение системы, учитывая, что
Квадрат любого выражения не может быть отрицательным . Поэтому это уравнение не имеет решений, а значит не имеет решений и система уравнений .
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: elenkakrutko
Предмет: Русский язык,
автор: nikitkaisaev2
Предмет: Русский язык,
автор: LisaRisa
Предмет: Математика,
автор: Аноним