Предмет: Геометрия,
автор: LordGavrik
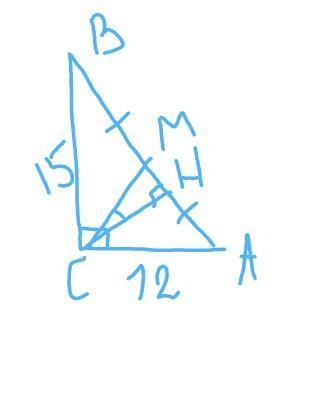
В прямоугольном треугольнике с катетами 12 и 15 из вершины прямого угла проведены медиана и высота.
Найдите тангенс угла между ними.
Ответы
Автор ответа:
0
Объяснение:
tg∠MCH=MH/CH
∆ABC - прямоугольный:
по теореме Пифагора:
АВ=√(ВС²+АС²)=√(15²+12²)=√369=3√41
по свойству медианы в прямоугольном тр-ке ,проведенной из вершины прямого угла:
СМ=АМ=МВ=1/2АВ=1/2×3√41=3/2×√41
S=1/2×AB×CH
CH=2S/AB
S=1/2×AC×BC=1/2×12×15=90
CH=2×90/3√41=60/√41=(60√41) /41
∆МНС -прямоугольный ,т.к СН-высота.
по теореме Пифагора:
МН=√(СМ²-СН²)=√((3/2×√41)²-(60/41×√41)²)=
=√(369/4-147600/1681)=√(369/4-3600/41)=
=√729/164=(27√41)/82
tg∠MCH=(27√41)/82:(60√41 )/41=
=27/82×41/60=27/2×1/60=27/120=9/40
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Oledghan
Предмет: Русский язык,
автор: Hdudgduc
Предмет: Русский язык,
автор: лиза2149
Предмет: Русский язык,
автор: noobasha11
Предмет: Русский язык,
автор: vladkeshan