Предмет: Математика,
автор: ruslanka1713
Розв’яжіть систему рівнянь
Приложения:
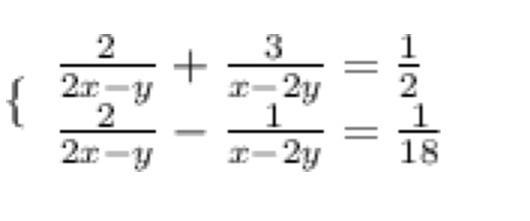
Ответы
Автор ответа:
2
Ответ:
Обозначим , тогда система
примет вид
.
Вычтем из первого уравнения второе , получим
Выразим х из второго уравнения и подставим в первое .
Причём получили значения переменных , которые удовлетворяют неравенствам .
Ответ: ( 5 ; -2) .
Похожие вопросы
Предмет: Русский язык,
автор: Аняняняняняня
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Treasury2007
Предмет: Литература,
автор: samira01427
Предмет: Русский язык,
автор: ichbestplayer