Предмет: Математика,
автор: kykyryza256
Решите пожалуйста два задания с фотографии. Заранее спасибо.
Приложения:
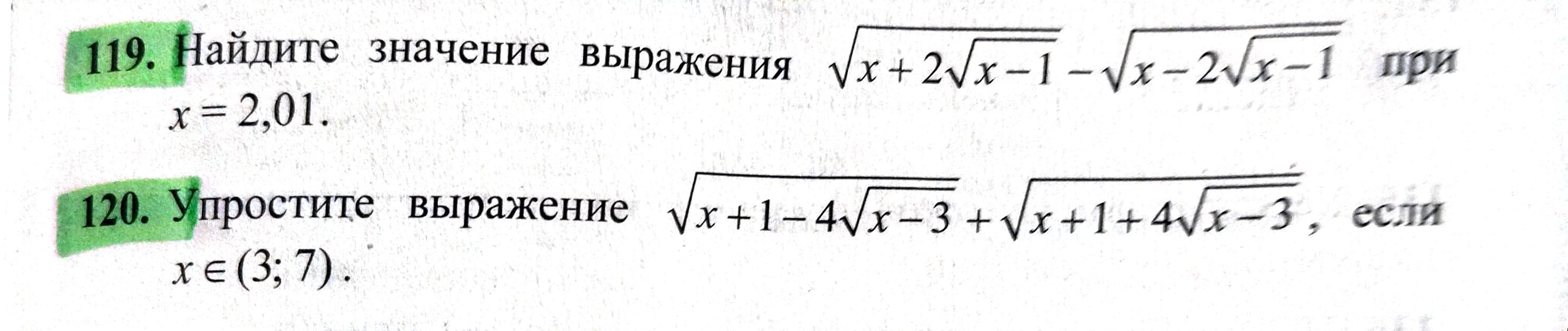
Ответы
Автор ответа:
1
kykyryza256:
Спасибо! Только вопрос, во втором задании в последней строке при раскрытии первого модуля не нужен минус? Там же получается |√х-3 - 2| отрицательное, нет?
нельзя просто убрать модульные скобки (и в первом задании тоже)) обязательно нужно учитывать, на каком промежутке модуль раскрываем (возможны ведь два варианта по определению)
1) √(х-1)>1 для х>2, потому √(х-1)-1>0 и |√(х-1)-1| = √(х-1)-1
2) 0<√(х-3)<2 для 3<х<7, потому √(х-3)-2<0 и |√(х-3)-2| = 2-√(х-3)... Ответ: 4
Похожие вопросы
Предмет: Окружающий мир,
автор: notkindi
Предмет: Окружающий мир,
автор: aliyahasenovna
Предмет: Окружающий мир,
автор: 70mamuka
Предмет: Русский язык,
автор: anastasia1979
Предмет: Русский язык,
автор: nestor2225