Предмет: Математика,
автор: Енонок
ПОМОГИТЕ ПОЖАЛУЙСТА
ОТВЕТ И ОБЪЯСНЕНИЕ
Приложения:
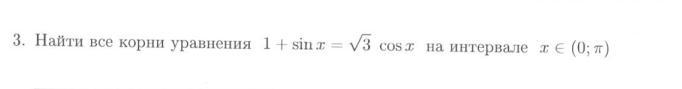
Ответы
Автор ответа:
0
Ответ:
Разделим уравнение на , тогда получим квадратное уравнение относительно
.
Вернёмся к переменной х .
c) Первая серия корней не входит в интервал .
А из второй серии корней в этот интервал входит .
Ответ:
Енонок:
откуда тут двойка вначале
формула синуса двойного угла: sinx=2*sin(x/2)*cos(x/2)
Похожие вопросы
Предмет: Русский язык,
автор: laskp2017
Предмет: Английский язык,
автор: натусик72
Предмет: Русский язык,
автор: gariko09
Предмет: Русский язык,
автор: nastyashilovich