Предмет: Математика,
автор: aram5541
Помогите не понимаю как решается
ОТВЕТ И ОБЪЯСНЕНИЕ
Приложения:
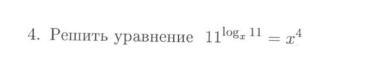
Аноним:
x - основание ?
х=0, х=1
Ответы
Автор ответа:
1
Ответ:
Прологарифмируем обе части равенства по основанию 11 .
Пользуемся свойством
Перейдём от основания х к основанию 11 по формуле
спасибо
пожалуйста
У вас есть телеграмм, чтоб вас не потерять на случаи если вы понадобитесь?
нет
ладно
я его удалила, много памяти жрёт
понял
Похожие вопросы
Предмет: Русский язык,
автор: поля20091
Предмет: Английский язык,
автор: good93
Предмет: Русский язык,
автор: Элина36913
Предмет: Русский язык,
автор: nik6712
Предмет: Математика,
автор: drhaus07p6k4ds