Question

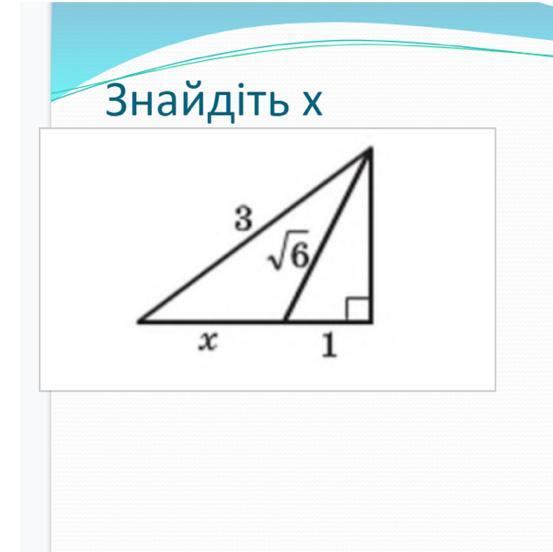
помогите пожалуйста

Answer 1

Ответ:

х = 1 ед.

Объяснение:

Дано:

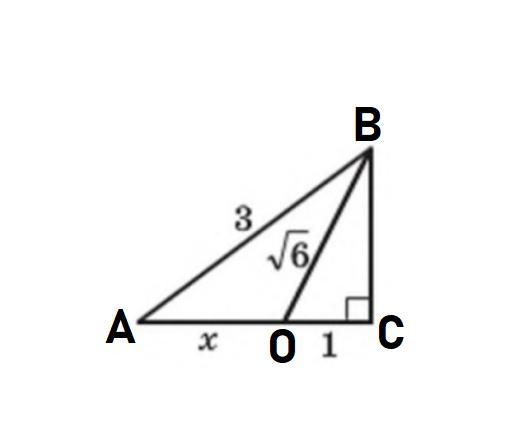
ΔАВС - прямоугольный (∠С = 90°) , ΔВОС - прямоугольный (∠С = 90°), АВ = 3 ед., ВО = √6 ед., ОС = 1 ед.

Найти:

АО = х

Решение:

Рассмотрим ΔВОС.

Найдем сторону ВС. Для этого применим теорему Пифагора:

BC² = BO² - OC², где

ВО - гипотенуза, ВС и ОС - катеты.

$BC = \sqrt{BO^{2} - OC^{2} }$

$BC = \sqrt{\sqrt{6}^{2} - 1^{2} } = \sqrt{6 - 1} = \sqrt{5}$ ед.

Теперь рассмотрим ΔАВС.

Найдем сторону АС через теорему Пифагора:

АС² = АВ² - ВС², где

АВ - гипотенуза, АС и ВС - катеты.

$AC = \sqrt{AB^{2} -BC^{2} }$

$AC = \sqrt{3^{2} - \sqrt{5}^{2} } = \sqrt{9 - 5 } = \sqrt{4} =2$ ед.

Найдем искомую сторону АО в ΔАВО:

АО = АС - ОС
АО = 2 - 1 = 1 ед.