Предмет: Математика,
автор: Izmaylov1
Надо найти корни уравнения
Приложения:
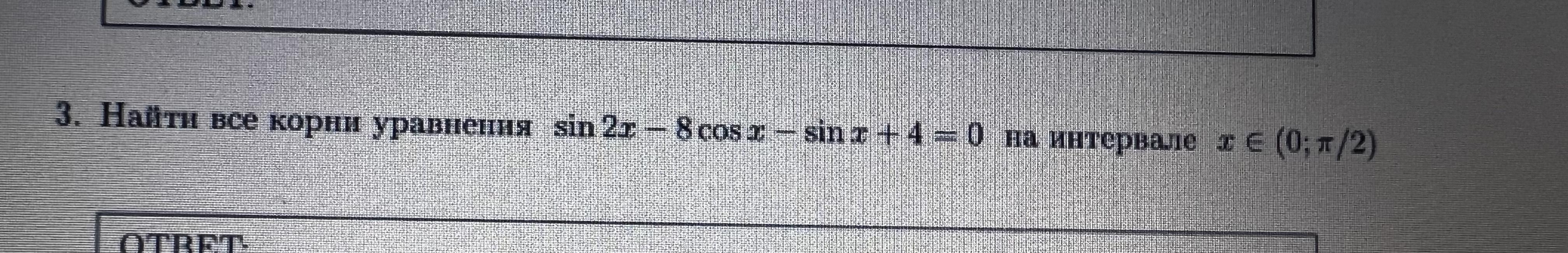
Ответы
Автор ответа:
1
Ответ:
х = π/3
Пошаговое объяснение:
Теория:
sin(2α) = 2sin(α)cos(α) - синус двойного угла
Решение:
sin(2x)-8cos(x)-sin(x)+4 = 0;
2sin(x)cos(x)-sin(x)-8cos(x)+4 = 0;
sin(x)*(2cos(x)-1)-4*(2cos(x)-1) = 0;
(sin(x)-4)(2cos(x)-1) = 0;
Произведение равно нулю, когда один из множителей равен нулю
Очевидно, что в промежутке х∈(0;π/2) лежит одно значение х = π/3
Похожие вопросы
Предмет: Русский язык,
автор: Incognito85
Предмет: Русский язык,
автор: Alëna099086
Предмет: Английский язык,
автор: охохохох
Предмет: Алгебра,
автор: Svizist
Предмет: Алгебра,
автор: natava7100