Question

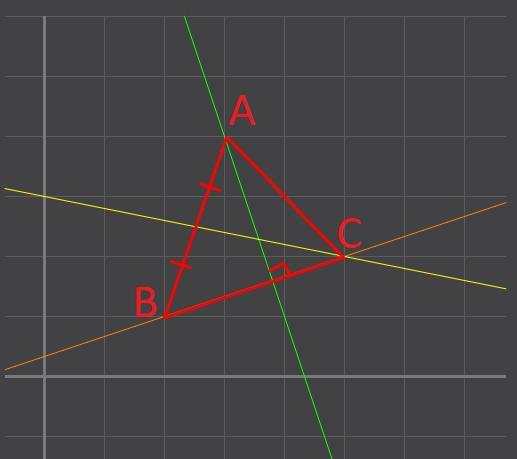
В треугольнике
ABC A(3; 4 ) В(2;1) С(5;2)
составьте
уравнения:
1) стороны BC
2) высоты, опущенной из вершины Aна сторону BC
3) медианы, проведенной из вершины C .

Answer 1

1. Для нахождения уравнения стороны ВС воспользуемся уравнением прямой, проходящей через две точки $(x_1;\ y_1)$ и  $(x_2;\ y_2)$:

$\dfrac{y-y_1}{y_2-y_1} =\dfrac{x-x_1}{x_2-x_1}$

Эти две точки: $B(2;\ 1)$ и $C(5;\ 2)$. Получим:

$\dfrac{y-1}{2-1} =\dfrac{x-2}{5-2}$

$\dfrac{y-1}{1} =\dfrac{x-2}{3}$

$3(y-1)=x-2$

$3y-3=x-2$

$3y=x+1$

$\boxed{y=\dfrac{1}{3} x+\dfrac{1}{3}}$

2. Высота АН является перпендикулярной к прямой ВС. Угловые коэффициенты перпендикулярных прямых являются обратными противоположными числами. Так как $k_{BC}=\dfrac{1}{3}$, то $k_{AH}=-3$. Воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом:

$y-y_0=k(x-x_0)$

Точка $A(3;\ 4)$, угловой коэффициент $k=-3$. Получим:

$y-4=-3(x-3)$

$y-4=-3x+9$

$\boxed{y=-3x+13}$

3. Найдем середину М отрезка АВ. Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка:

$x_M=\dfrac{x_A+x_B}{2} =\dfrac{3+2}{2} =2.5$

$y_M=\dfrac{y_A+y_B}{2} =\dfrac{4+1}{2} =2.5$

Вновь воспользуемся уравнением прямой, проходящей через две точки: $C(5;\ 2)$ и $M(2.5;\ 2.5)$.

Получим:

$\dfrac{y-2}{2.5-2} =\dfrac{x-5}{2.5-5}$

$\dfrac{y-2}{0.5} =\dfrac{x-5}{-2.5}$

$y-2 =\dfrac{x-5}{-5}$

$-5(y-2) =x-5$

$-5y+10 =x-5$

$-5y =x-15$

$\boxed{y =-\dfrac{1}{5} x+3}$