Question

Діагоналі ромба дорівнюють а і 3 корінь а. знайдіть більший кут ромба

Answer 1

Доброго ранку. До Вашої уваги розв'язання задачі.

Answer 2

Ответ:

Больший угол ромба равен 120°.

Объяснение:

Диагонали ромба равны а и а√3. Найдите больший угол ромба.

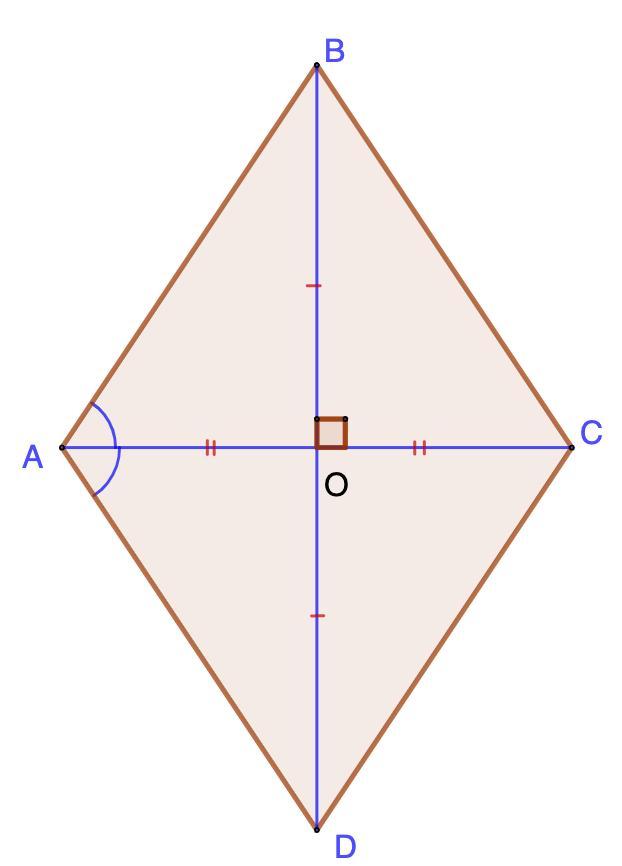
Дано: ABCD - ромб;

АС и BD - диагонали;

AC = a; BD = a√3.

Найти: ∠А.

Решение:

Рассмотрим ΔАВО.

• Диагонали ромба взаимно перпендикулярны.

⇒ ΔАВО - прямоугольный.

• Диагонали ромба точкой пересечения делятся пополам.

⇒

$\displaystyle \bf {AO=OC=\frac{a}{2} }\\\\BO=OD=\frac{a\sqrt{3} }{2}$

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle \bf tg\angle{BAO}=\frac{BO}{AO} =\frac{a\sqrt{3}\cdot{2} }{2\cdot{a}} =\sqrt{3}$

⇒ ∠BAO = arctg (√3) = 60°

• Диагонали ромба являются биссектрисами его углов.

⇒ ∠ВАО = ∠OAD = 60°

Тогда ∠А = ∠ВАО + ∠OAD = 120°

Больший угол ромба равен 120°.