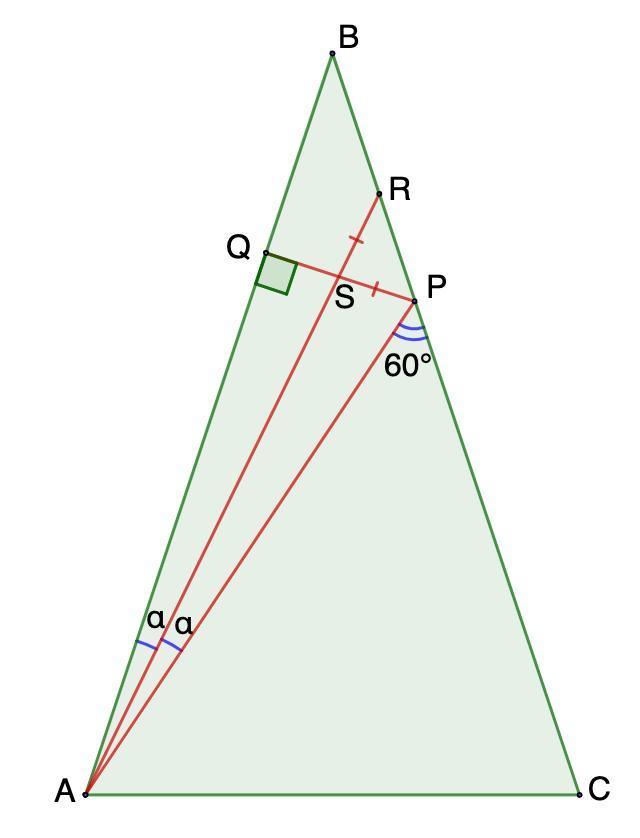
Дан равнобедренный треугольник ABC (AB = BC). Точка P на стороне BC такова, что угол APC = 60градусов. Высота PQ и биссектриса AR треугольника APB пересекаются в точке S. Оказалось, что PS = SR. Чему равен угол ABC?
Ответы
Ответ:
Угол АВС равен 40°.
Объяснение:
Дан равнобедренный треугольник ABC (AB = BC). Точка P на стороне BC такова, что угол APC = 60°. Высота PQ и биссектриса AR треугольника APB пересекаются в точке S. Оказалось, что PS = SR. Чему равен угол ABC?
Дано: ΔАВС - равнобедренный;
Р ∈ ВС, ∠APC = 60°;
PQ - высота, AR - биссектриса ΔАРВ;
PQ ∩ AR = S;
PS = SR.
Найти: ∠АВС.
Решение:
Пусть ∠BAR = ∠RAP = α (AR - биссектриса ΔАРВ)
1. Рассмотрим ΔARP.
∠APC = 60° - внешний.
- Внешний угол треугольника равен сумме двух углов, не смежных с ним.
⇒ ∠ARP = 60° - α
2. Рассмотрим ΔABP.
∠APC = 60° - внешний.
⇒ ∠ABC = 60° - 2α (1)
3. Рассмотрим ΔSRP.
PS = SR (условие)
⇒ SRP - равнобедренный.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠SPR = ∠ARP = 60° - α
4. Рассмотрим ΔQBP.
PQ - высота ΔАРВ.
⇒ ΔQBP - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠АВС = 90° - ∠SPR = 90° - 60° + α = 30° + α (2)
5. Приравняем выражения (1) и (2) и найдем α:
60° - 2α = 30° + α
3α = 30°
α = 10°
⇒ ∠АВС = 30° + α = 30° + 10° = 40°.
Угол АВС равен 40°.