ПОМОГИТЕ ПОЖАЛУЙСТА
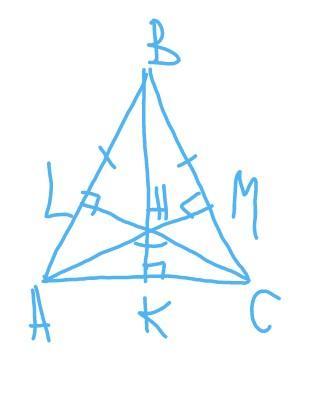
У рівнобедреному трикутнику АВС кут АНС дорівнює 126°, де Н – ортоцентр трикутника АВС. Знайдіть кути трикутника АВС. Скільки розв’язків має задача?
Ответы
Объяснение:
ортоцентр -точка пересечения прямых,содержащих высоты треугольника.
<LHM=<AHC=126° - как вертикальные.
LBMH -четырехугольник.
<В=360-<LHM-<BLC-<BMA=
=360-126-90-90=54°
<ВАС=<ВСА=(180-<В):2=(180-54):2=63°
ответ: 63;63;54
Высота в равнобедренном треугольнике является биссектрисой и медианой
∆АНС - равнобедренный
<НАС=<НСА=(180-<АНС):2=(180-126):2=
=27°
∆АМС-прямоугольный,т.к АМ -высота
<МСА=90-<НАС=90-27=63°
<ВСА=<МСА=63°
<ВАС=<ВСА=63°,т.к ∆АВС -равнобедренный.
<АВС=180-2×<ВАС=180-2×63=54°
ответ: 63°;63°54°
2 решение:
АВ=АС:
∠АНС=126°
∠АНL=180-∠AHC=180-126=54° т.к сумма смежных углов равна 180°.
∆АНL -прямоугольный:
Cумма острых углов в прямоугольном тр-ке равна 90°.
∠LAH=90-∠АНL=90-54=36°.
В равнобедренном треугольнике высота является биссектрисой, значит
∠А=2×∠LAH=2×36=72°.
В равнобедренном треугольнике углы при основании равны:
∠В=∠С=(180-∠А)=(180-72):2=54°
ответ: 72°;54°; 54°;