Question

чи є точка (1;1) центром кола яке проходить через точки (5;4) та (4;-3)

Answer 1

Ответ:

Точка (1;1) является центром окружности, проходящей через точки  (5;4) и (4;-3)

Объяснение:

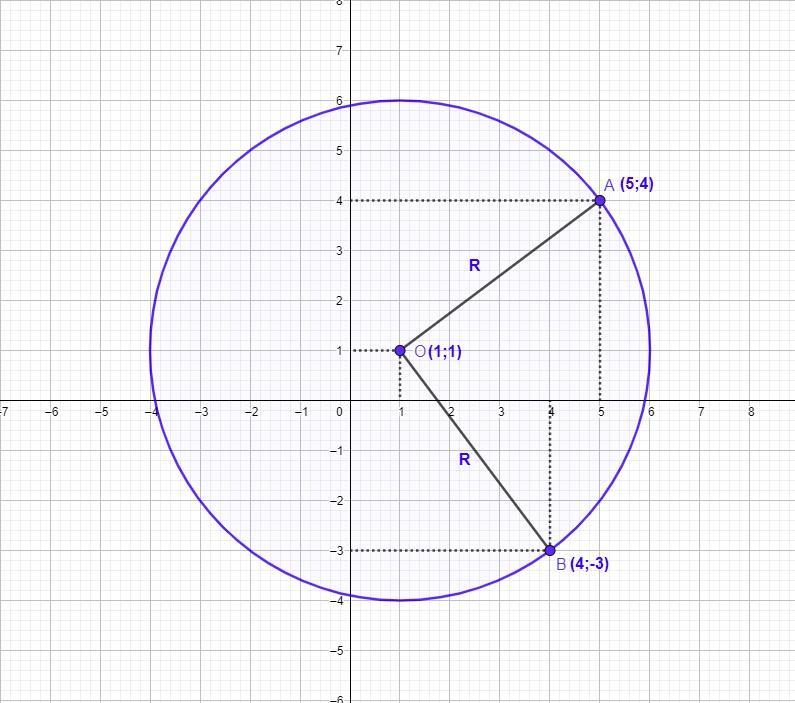
По условию задачи точки А(5;4) и В(4;-3) лежат на окружности. Нам надо проверить, является ли точка О(1;1) её центром.

Радиус окружности — отрезок, который соединяет центр окружности и любую точку на ней.

Нам надо найти длину отрезков АО и ВО, и если они будут равны, то АО и ВО будут радиусами окружности с центром в точке О(1;1).

Найдём длину отрезка АО:

$AO=\sqrt{(x_O-x_A)^{2}+(y_O-y_A)^{2} } =\\\\=\sqrt{(1-5)^{2} +(1-4)^{2} } =\sqrt{16+9} =\sqrt{25} =5$

Найдём длину отрезка BО:

$BO=\sqrt{(x_O-x_B)^{2}+(y_O-y_B)^{2} } =\\\\=\sqrt{(1-4)^{2} +(1-(-3))^{2} } =\sqrt{9+16} =\sqrt{25} =5$

Как мы видим, АО=ВО=5. Значит АО и ВО - радиусы окружности, а точка О(1;1) - её центр.