Question

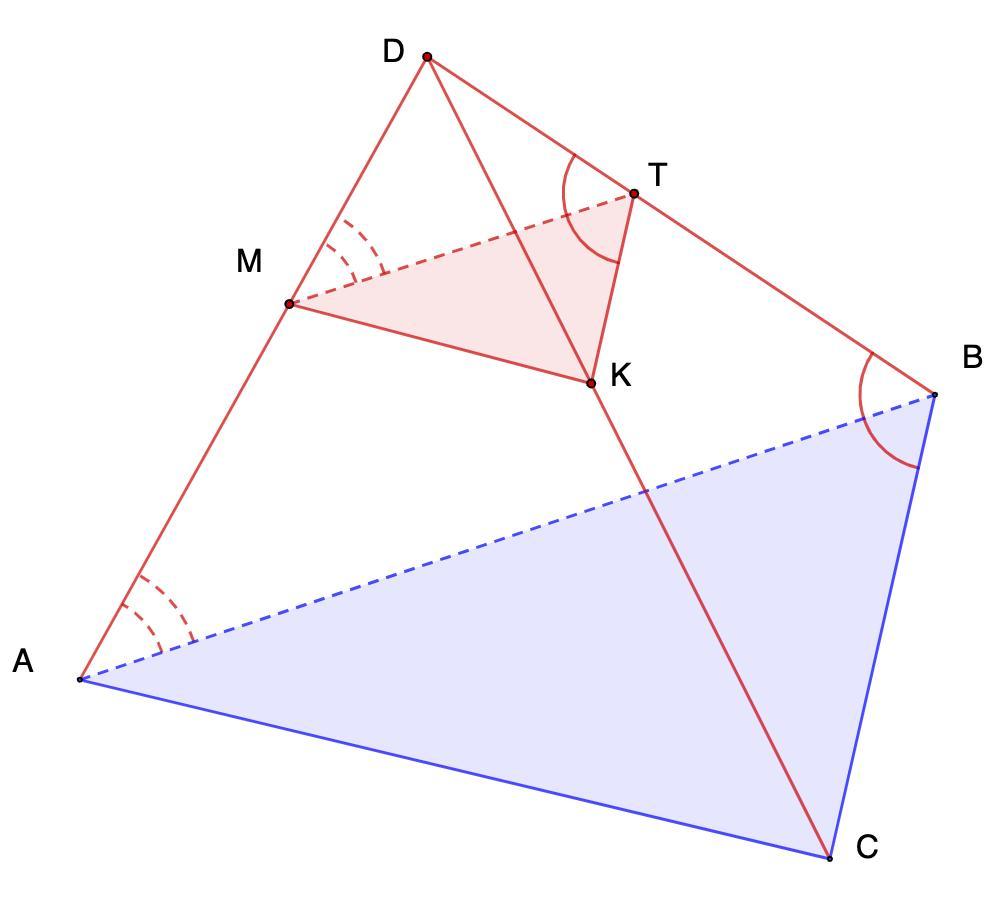
Точка D не належить площині трикутникаABC.Точки M,T,K належать відрізкам DA,DB,DC відповідно і такі що DAB=DMT,DTK=DBC.Довести що площина MTK паралельна площині ABC
З малюнком будь ласка

Answer 1

Ответ:

Доказано, что плоскость MTK параллельна плоскости ABC.

Объяснение:

Точка D не принадлежит плоскости треугольника.Точки M, T, K принадлежат отрезкам DA, DB, DC соответственно и такие что ∠DAB = ∠DMT, ∠DTK = ∠DBC. Доказать что плоскость MTK параллельна плоскости ABC.

Дано: ΔАВС;

D ∉ ABC;

M ∈ DA; T ∈ DB; K ∈ DC;

∠DAB = ∠DMT, ∠DTK = ∠DBC.

Доказать:  MTK || ABC.

Доказательство:

Вспомним:

• Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

1. Рассмотрим ΔADB.

∠DAB = ∠DMT - соответственные при МТ и АВ и секущей AD.

⇒ МТ || АВ.

2. Рассмотрим ΔСDB.

∠DTK = ∠DBC - соответственные при КТ и ВС и секущей DB.

⇒ КТ || ВС

3. MT ∩ TK = T

AB ∩ BC = B

При этом МТ || АВ, КТ || ВС;

⇒ MTK || ABC.

Доказано, что плоскость MTK параллельна плоскости ABC.

#SPJ1