Предмет: Математика,
автор: only4ldoe1337
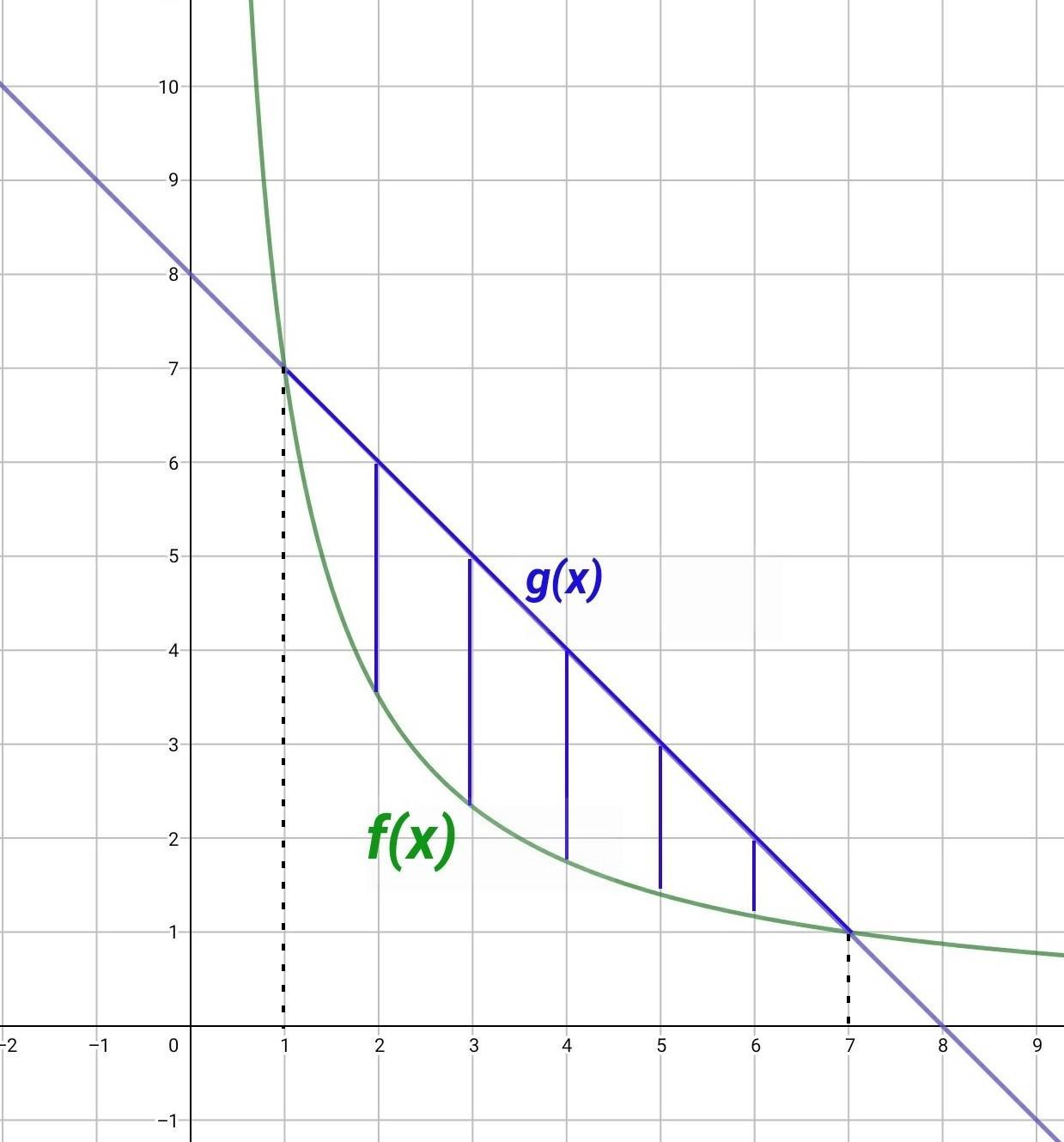
Знайти площу фігури, обмеженої лініями 
должен быть рисунок, на котором заштрихована фигура, площадь которой находим
Ответы
Автор ответа:
0
Ответ:
36
Пошаговое объяснение:
y=7/x,
y=8-x
Пусть f(x)=7/x, g(x)=8-x
Найдём абсциссы точек пересечения графиков функций (пределы интегрирования):
8-х=7/х
8-х-7/х=0
х²-8х-7=0
х=1 или х=7
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Alexandra123789456
Предмет: Українська мова,
автор: White77
Предмет: Английский язык,
автор: hellokatedale
Предмет: Английский язык,
автор: haydaydva400
Предмет: Українська мова,
автор: Ogurei