Предмет: Математика,
автор: rulikk90
Диференціювати y= 2^sinx * arcsin2x
Приложения:
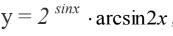
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
(a^x)'=a^xlna
(f(x)*g(x))'=f'(x)g(x)+g'(x)f(x)
(2^sinx*arcsin2x)'=2^(sinx)*ln2*(sinx)'*arcsin2x+
+2^sinx*(2x)'*1/sqrt(1-4x²)=cosx*2^(sinx)*ln2*arcsin2x+
+2*2^sinx/sqrt(1-4x²)=2^sinx(cosx*arcsin2x*ln2+2/sqrt(1-4x²))
Похожие вопросы
Предмет: Русский язык,
автор: JuliaKuki
Предмет: Другие предметы,
автор: Sus1985
Предмет: Русский язык,
автор: ket851230
Предмет: Французский язык,
автор: a123550
Предмет: Алгебра,
автор: dernovwarface