Question

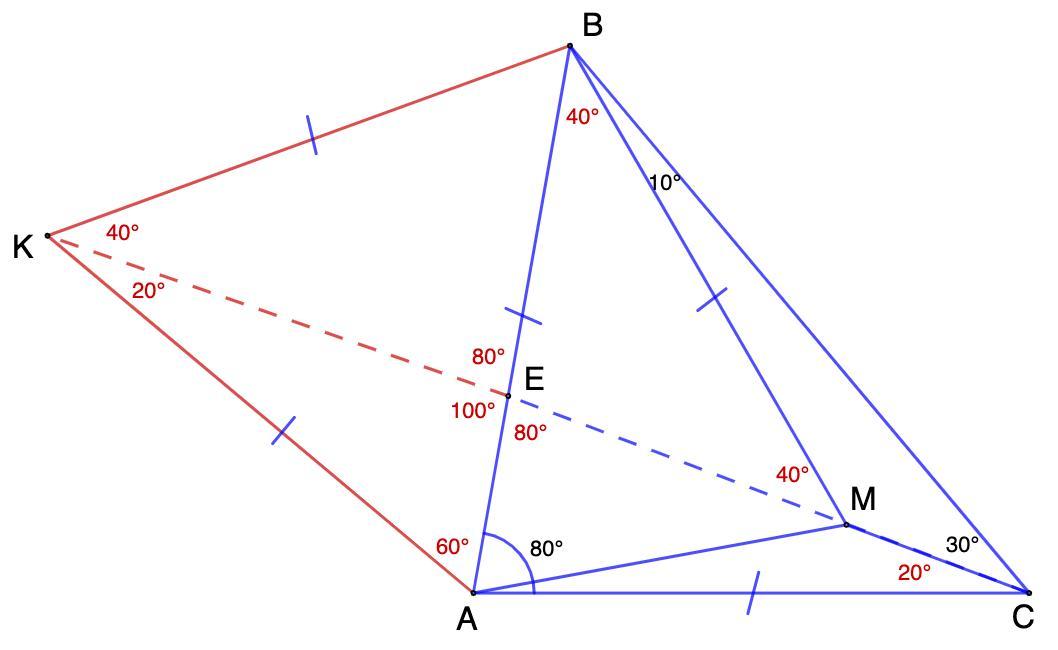
У трикутнику АВС АВ=АС, кут ВАС=80°. Усередині трикутника взята така точка М, що кут МВС=10°, кут МСВ=30°. Знайдіть кут АМВ.

Answer 1

Ответ:

Угол АМВ равен 70°.

Объяснение:

В треугольнике АВС АВ = АС, угол ВАС=80°. Внутри треугольника взята такая точка М, что угол МВС = 10°, угол МСВ = 30°. Найдите угол АМВ.

Дано: ΔАВС;

АВ = АС;

∠МВС = 10°; ∠МСВ = 30°.

Найти: ∠АМВ.

Решение:

1. Рассмотрим ΔАВС.

АВ = АС (условие)

⇒ΔАВС - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠АВС = ∠АСВ

• Сумма углов треугольника равна 180°.

⇒ ∠АВС = ∠АСВ = (180° - 80°) : 2 = 50°

2. На стороне АВ построим равносторонний ΔАКВ.

Соединим точки С и К.

Рассмотрим ΔАКС.

АВ = АС (условие)

АВ = АК (построение)

⇒ АС = АК

⇒ ΔАКС - равнобедренный.

∠КСА = ∠АСВ - ∠ВСМ = 50° - 30° = 20°

∠КСА  = ∠АКС = 20°

3. Продлим СМ до пересечения с АВ и поставим точку Е.

Соединим Е и К.

Рассмотрим ΔАКЕ.

∠АЕК = 180° - ∠АКЕ - ∠КАЕ = 180° - 20° - 60° = 100°

Рассмотрим ΔАЕС.

∠АЕС = 180° - ∠ЕАС - ∠АСЕ = 180° - 80° - 20° = 80°

∠АЕК + ∠АЕС = 100° + 80° = 180°

⇒ ∠АЕК и ∠АЕС - смежные.

Значит точки К, Е, М, С лежат на одной прямой.

4. Рассмотрим ΔКВМ.

∠МКВ = ∠АКВ - ∠АКЕ = 60° - 20° = 40°

• Внешний угол треугольника равен сумме двух углов, не смежных с ним.

∠ВМК = ∠МВС + ∠ВСМ = 10° + 30° = 40°

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ КВ = ВМ

5. Рассмотрим ΔАВМ.

ВМ = КВ (п.4)

АВ = КВ (построение)

⇒ ΔАВМ - равнобедренный.

⇒ ∠ВАМ = ∠АМВ.

∠ АВМ = ∠АВС - ∠МВС = 50° - 10° = 40°

⇒ ∠ВАМ = ∠АМВ = (180° - 40°) : 2 = 70°

Угол АМВ равен 70°.

#SPJ1