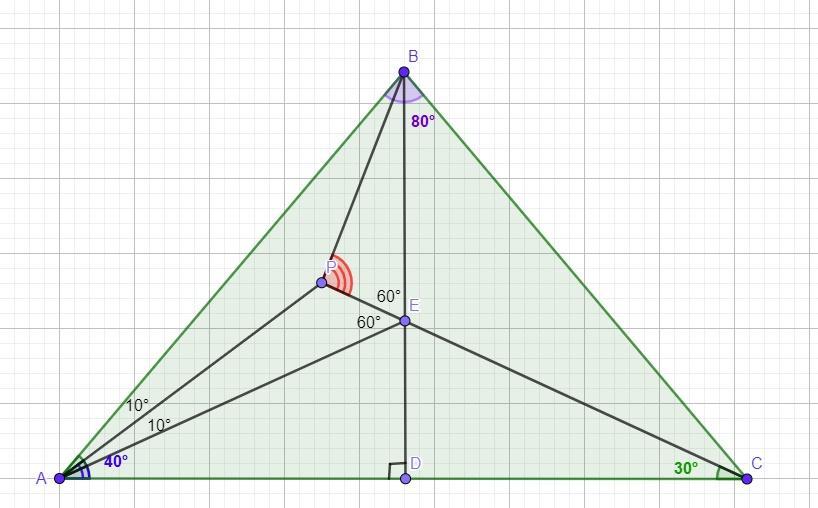
30. ТочкаP лежить усередині рівнобедреного трикутника ABC(AB=BC),
причому кут ABC=80°, кут PAC=40°, кут ACP=30°. Знайдіть кут BPC.
Ответы
Ответ:
∠ BPC = 100°
Объяснение:
ΔABC - равнобедренный, с основанием АС. Боковые стороны:AB=BC,
∠ABC=80°, ∠PAC=40°, ∠ACP=30°. Требуется найти ∠BPC.
1) В равнобедренном треугольнике углы при основании равны:
∠А=∠С=(180°-∠В) ÷ 2 = (180°-80°) ÷ 2 = 50°
∠ВАР=∠А-∠PAC= 50°-40°=10°
2)Проведём высоту ВD в равнобедренном ΔАВС. ВD⊥АС. Точка Е - точка пересечения отрезка СР с высотой ВD.
Так как в равнобедренном треугольнике высота является также биссектрисой и медианой, то ВD - биссектриса ∠В: ∠АВD=∠СВD=40°. АD=DС, а ΔЕDА=ΔЕDС по двум катетам. ⇒ ∠ЕАD=∠АСР=30°
∠РАЕ=∠РАС-∠ЕАD=40°-30°=10°
∠ВАР=∠РАЕ=10°, следовательно АР - биссектриса ∠ВАЕ ΔАВЕ.
3) По теореме о внешнем угле треугольника:
∠АЕР=∠ЕАС+∠ЕСА=30°+30°=60° (∠АЕР - внешний угол ΔАЕС)
∠АЕВ=∠ЕАD+∠АDЕ=30°+90°=120° (∠АЕВ - внешний угол ΔАЕD)
⇒ ∠ВЕР=∠АЕВ- ∠АЕР=120°-60°=60°
∠ВЕР= ∠АЕР=60°. Следовательно ЕР - биссектриса ∠АЕВ ΔАВЕ.
Следовательно точка Р - точка пересечения биссектрис ΔАВЕ.
ВР - биссектриса ∠АВЕ.
∠ЕВР=∠АВР=40° ÷ 2 = 20°
4) ΔВРЕ.
∠РРЕ=∠ВРС=180°-∠ЕВР-∠ВЕР=180°-20°-60°=100°
#SPJ1