Предмет: Математика,
автор: rulikk90
Диференціювати ![\frac{ 7\sqrt[3]{x} - (3x + 6)}{\sqrt[3]{x} } \frac{ 7\sqrt[3]{x} - (3x + 6)}{\sqrt[3]{x} }](https://tex.z-dn.net/?f=%5Cfrac%7B+7%5Csqrt%5B3%5D%7Bx%7D+-+%283x+%2B+6%29%7D%7B%5Csqrt%5B3%5D%7Bx%7D+%7D)
Приложения:
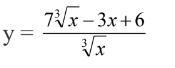
Ответы
Автор ответа:
0
Відповідь:
Покрокове пояснення:
Для диференціювання даного прикладу використаємо наступні формули:
Перепишу, замінивши корені відповідними степенями
Диференціюю по правилу диференціювання частки:
Похожие вопросы
Предмет: Другие предметы,
автор: Музыка111111
Предмет: Қазақ тiлi,
автор: Aruzhan20062006
Предмет: Русский язык,
автор: НМИ2003
Предмет: Биология,
автор: belinskiy10sadie