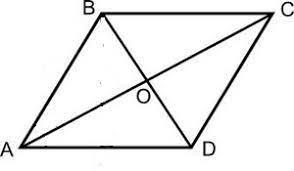
Почему ,если периметр четырехугольника 12см, то какая-то из перечисленных величин (1см, 3см, 5см, 7см) НЕ МОЖЕТ БЫТЬ длиной диагонали?
Ответы
По властивостях треугольника длина одной стороны не может быть больше сумы двух остальных.
Так как диагональ разделяет четырехугольник на 2 треугольника, то она не может быть больше сумы 2 сторон с одной стороны ее, или суммы двух других сторон. А они в среднем дают 6см.
(Очевидно, что если сумма 2 сторон с одной стороны больше 6, то с другой меньше, например 7 и 5, или 8 и 4)
То получается, что аж никак не может быть 7 см длина диагонали.
Ответ:
Пошаговое объяснение:
Рассмотрим ромб со стороной AB=3 см и большей диагональю AC=5 см.
AO=0,5AC=2,5 см
BO²=AB²-AO²=3²-2,5²=9-6,25=2,75
BO=√2,75=0,5√11
BD=2BO=√11
Так что такой четырехугольник существует.
Так же возможны варианты 1 см и 3 см. BD=1 см или 3 см можно рассмотреть так же.
Соединим два равносторонних треугольника со стороной 3 см. Получим ромб одна из диагоналей которого равна 3 см.
Невозможен только вариант 7 см.
Если AC=7 см
AB+BC>AC
CD+AD>AC
P=(AB+BC)+(CD+AD)>7+7=14
12=P>14-противоречие