Предмет: Математика,
автор: kornijcuknazarij13
Допоможіть будь ласка.
Завдання на фото. Даю 50б.
Приложения:
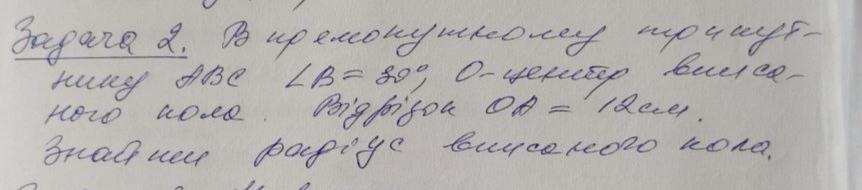
Ответы
Автор ответа:
1
Ответ:
6 cм
Пошаговое объяснение:
ΔАВС - прямоугольный, ∠С=90°, ∠В=30°, О - центр вписанной окружности с радиусом r. АО=12см. Найти: r.
Сумма острых углов в прямоугольном треугольнике равна 90° ⇒
∠А=90°-∠В=90°-30°=60°
Так как радиус вписанной окружности лежит на пересечении биссектрис, то АО - биссектриса ∠А. ⇒∠ОАМ=∠ОАК=60°:2=30°
Окружность касается гипотенузы АВ в точке К, а катета АС в точке М. АС и АВ - касательные к окружности в с центром в т.О, МО=КО=r - радиусы окружности ⇒ МО⊥АС, КО⊥АВ - по свойству касательных к окружности.
В прямоугольном ΔАМО катет МО лежит напротив угла ∠ОАМ=30° ⇒
МО равен половине гипотенузы АО:
r = МО = 1/2 * АО = 1/2 * 12 = 6 см
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Friends2017
Предмет: Русский язык,
автор: роза345
Предмет: Английский язык,
автор: Дима1471367i
Предмет: История,
автор: Yanka08