Предмет: Математика,
автор: genipar852
ПОМОЖИТЕ ПОЖАЛУЙСТА!!!!!!!
СРОЧНО НУЖНО
РОМА
Приложения:
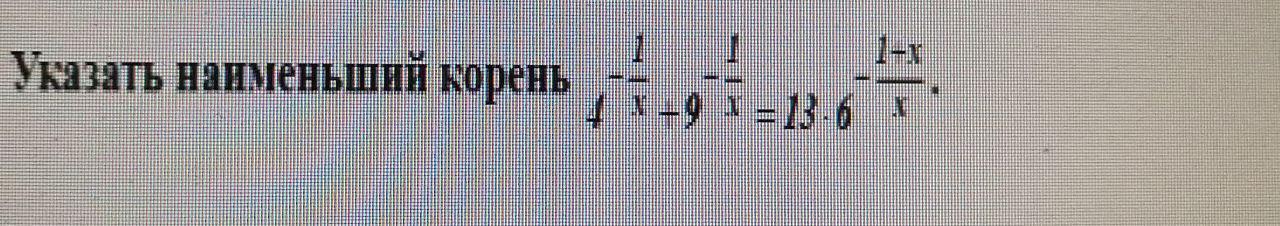
Ответы
Автор ответа:
0
Ответ:
Разделим обе части равенства на .
Введём замену переменной . Тогда уравнение примет вид
Вернёмся к старой переменной.
Похожие вопросы
Предмет: Английский язык,
автор: ambiguous
Предмет: Русский язык,
автор: Valya7002
Предмет: Окружающий мир,
автор: oksanka244
Предмет: Математика,
автор: katyaakimhano
Предмет: История,
автор: alenazhurba1