Предмет: Геометрия,
автор: Аноним
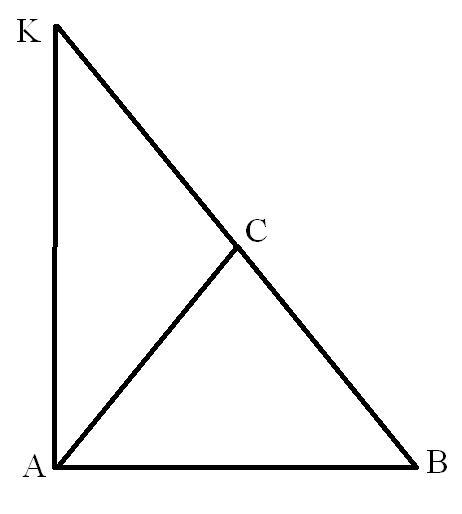
Кут С при вершині рівнобедреного трикутника АВС дорівнює 80°. Бічна сторона ВС продовжена за вершину на відрізок СК, рівний ВС. Доведіть, що відрізок АК перпендикулярний АВ та АК > АВ.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
AC=BC=CK⇒точки A, B и K равноудалены от точки C.
Значит точка C является центром окружности описанной около ΔABK, где отрезок AB - диаметр. Из чего следует, что ∠KAB=90°
∠KAB=90°⇒AK⊥AB
AC=BC⇒ΔABC - равнобедренный⇒∠CAB=∠CBA=0,5(180°-∠ACB)=50°
В ΔABK ∠A=90°
∠AKB=90°-∠CBA=90°-50°=40°
∠AKB=40°<50°=∠KBA⇒∠AKB<∠KBA⇒AB<AK
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: KSENIA111222333
Предмет: Қазақ тiлi,
автор: абаткадыр
Предмет: Окружающий мир,
автор: Катя20124
Предмет: Обществознание,
автор: Аноним
Предмет: Музыка,
автор: AssortyDuetovich