IMG_2022070
5_233536.jpg

Ответы
Ответ:
1 - А, 2 - Б, 3 - Г
Пошаговое объяснение:
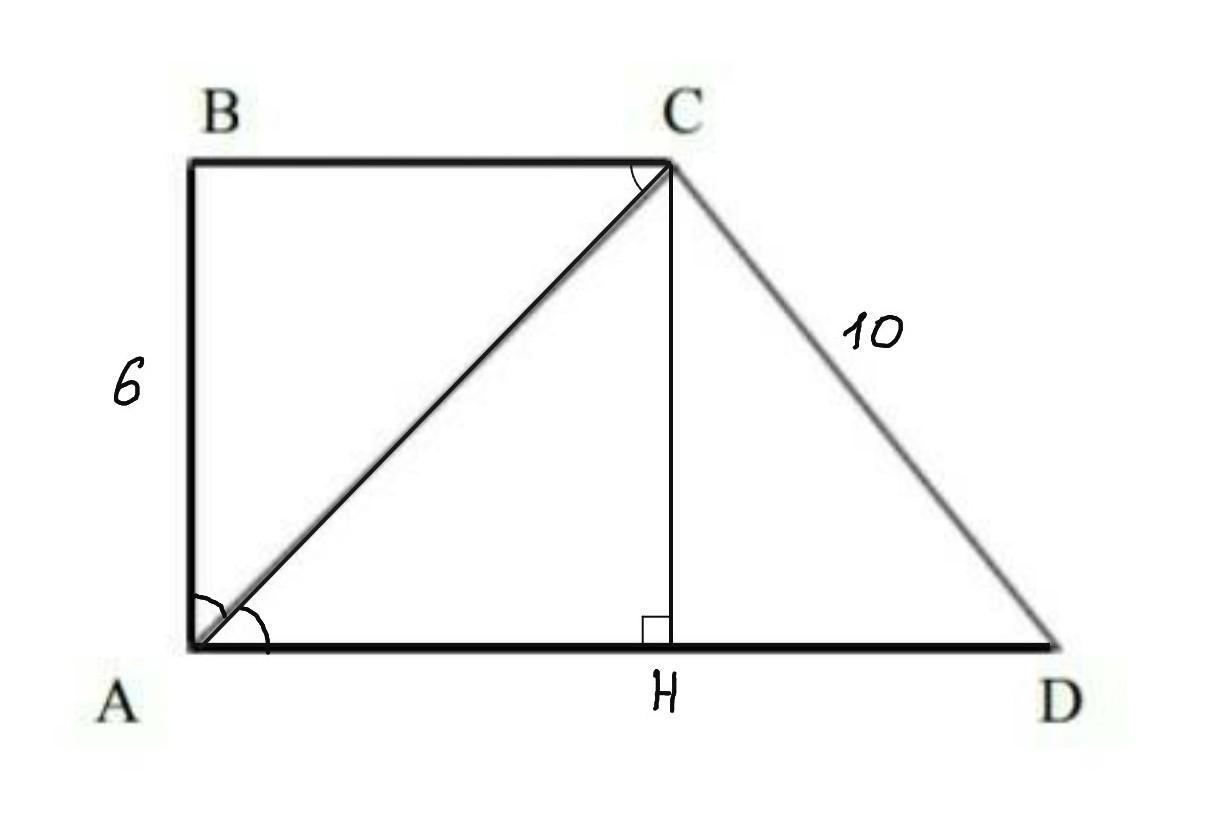
1) Найдём ВС
∠CAD=∠ACB - как внутренние накрест лежащие углы при параллельных прямых BC и AD и секущей AC.
∠BAC=∠CAD - так как AC - биссектриса ∠А.
Следовательно ∠BAC=∠ACB, а △ABC - равнобедренный с основанием AC и боковыми сторонами AB и BC. Значит AB=BC= 6 см (по определению равнобедренного треугольника)
Ответ А
2) Найдём проекцию CD на AD.
Проведём CH⟂AD. CH - высота, CD - наклонная, HD - проекция наклонной CD на AD.
△CHD - прямоугольный, ∠H=90°. CD=10 см - по условию, CH=AB ( по свойству прямоугольника), по теореме Пифагора найдём HD:
HD²=CD²_CH²=10²-6²=100-36=64
HD=√64=8см
Ответ Б
3) Найдём среднюю линию трапеции m
AD=AH+HD.
AH=BC=6см - по свойству прямоугольника.
AD=6+8=14см
Среднюю линию трапеции находим по формуле:
см
Средняя линия трапеции равна 10 см.
Ответ Г