Предмет: Алгебра,
автор: dilnura0518
pleaseeeeeeeeeeeeeee
Приложения:
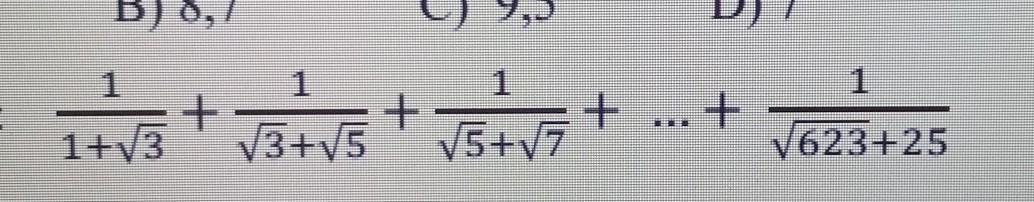
Ответы
Автор ответа:
1
Ответ:
Возьмем под корень 25=√625.
Теперь надо избавиться от всех иррациональностей в знаменателях.
В знаменателе получится разность квадратов a²-b²=(a-b)(a+b)
А теперь проделаем такое со всеми дробями.
Как мы видим у всех в знаменателях получаются 2, поэтому его можно вывести за скобку.
Противоложные числа под корнем, такие как √3-√3, √5-√5, √7-√7 и т.д до √623-√623, взаимно уничтожаются
И в конце остаются только
Ответ: 12
Похожие вопросы
Предмет: Қазақ тiлi,
автор: нина2311
Предмет: Окружающий мир,
автор: НАСТЯБАДАН
Предмет: Английский язык,
автор: Айыма1
Предмет: Биология,
автор: lilyok2006
Предмет: Литература,
автор: Kamilauz