Предмет: Алгебра,
автор: lllll58
помогите решить пожалуйста, если можно словами тоже чутка объяснить:^)
Приложения:
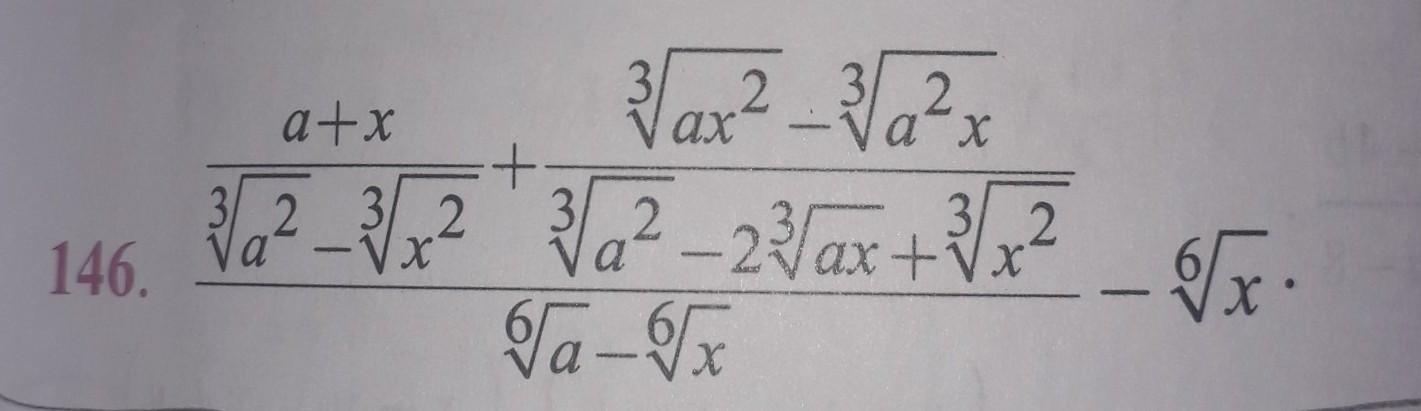
Ответы
Автор ответа:
2
Ответ:
.
Чтобы не загромождать запись корнями различных степеней переобозначим , тогда выражение перепишем в виде:
.
В знаменателе получили разности квадратных корней, так как
. Аналогично,
Далее при преобразовании выражения пользуемся формулами сокращённого умножения : суммой кубов, квадратом разности, разностью квадратов .
lllll58:
огромное спасибо:^)
пожалуйста :)
отмечай лучший ответ
хорошо
Похожие вопросы
Предмет: Русский язык,
автор: 5минут1
Предмет: Русский язык,
автор: Аноним
Предмет: Черчение,
автор: TikhopletXei
Предмет: Обществознание,
автор: qwewqe9494
Предмет: Алгебра,
автор: sm473086