Предмет: Алгебра,
автор: ananimanani87
Данный интеграл имеет решение?
Если есть решение написать его.
БЕЗ СПАМА!!!!
Приложения:
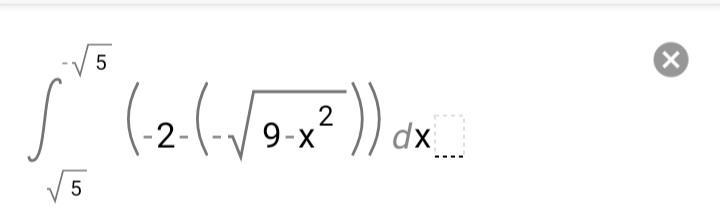
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ: 9-x²≥0 (3+x)*(3-x)≥0 x∈[-3;3] [-√5;√5] ∈ [-3;3].
Подинтегральная функция является чётной функцией (f(-x)=f(x)).
Так как пределы симметричные ⇒ запишем интеграл, как удвоенный интеграл по половинному промежутку:
Похожие вопросы
Предмет: Українська мова,
автор: ura21penoza211
Предмет: Другие предметы,
автор: irka0022
Предмет: Русский язык,
автор: 10Veronika10
Предмет: Литература,
автор: masavolkova13