Предмет: Геометрия,
автор: kamilmatematik100504
.......................................
Приложения:
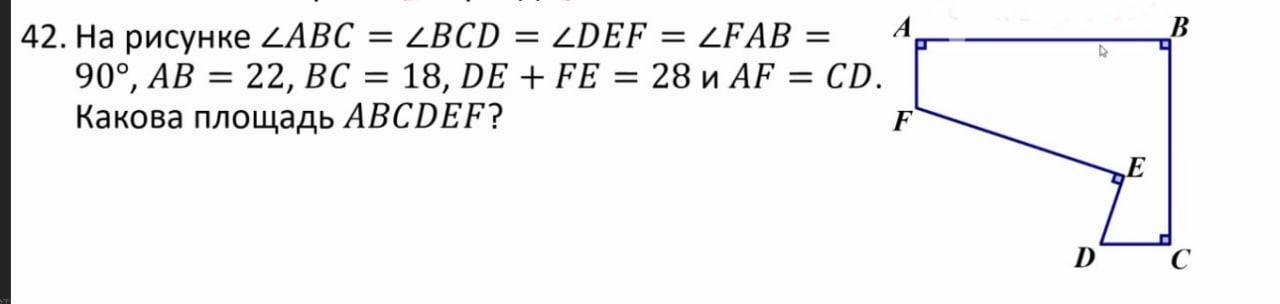
Ответы
Автор ответа:
2
Ответ:
204 кв. ед.
Объяснение:
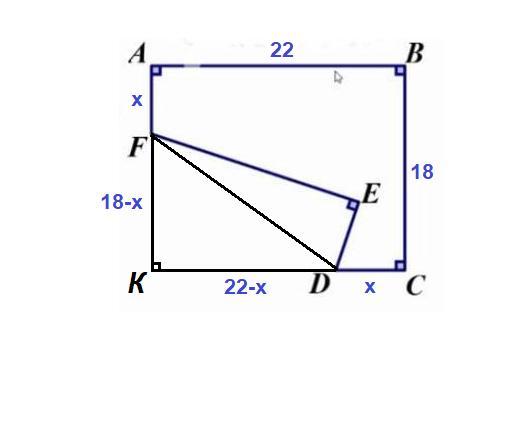
Дочертим фигуру до прямоугольника АВСК.
AF = CD = x
FK = 18 - x
KD = 22 - x
Чтобы найти площадь ABCDEF, можно от площади прямоугольника АВСК отнять площади двух треугольников: FED и FKD.
DE + FE = 28
Возведем равенство в квадрат:
DE² + 2DE·FE + FE² = 784
Учитывая, что DE² + FE² = FD² по теореме Пифагора из прямоугольного треугольника FED, а
, получаем:
(1)
С другой стороны из прямоугольного треугольника FKD:
FD² = FK² + DK² = (18 - x)² + (22 - x)²
FD² = 324 - 36x + x² + 484 - 44x + x² = 2x² - 80x + 808
Подставим в (1):
Выразим через х площадь треугольника FKD:
Тогда сумма площадей треугольников FED и FKD:
Площадь прямоугольника ABCK:
Тогда площадь ABCDEF:
Приложения:
BMW52:
Предполагали что-то ли, что сумма площадей будет конкретное число? Или как?
Можно было решить намного проще собрав четыре такие фигуры вместе , но я хотел увидеть альтернативный метод https://prnt.sc/fzbA2luJGJIV
Похожие вопросы
Предмет: Русский язык,
автор: YULIANA505
Предмет: Русский язык,
автор: БелаяЧайка
Предмет: Английский язык,
автор: deryten
Предмет: Физика,
автор: ATOM34
Предмет: Физика,
автор: Nastt0106