Предмет: Алгебра,
автор: dilnura0518
can you solve this question
Приложения:
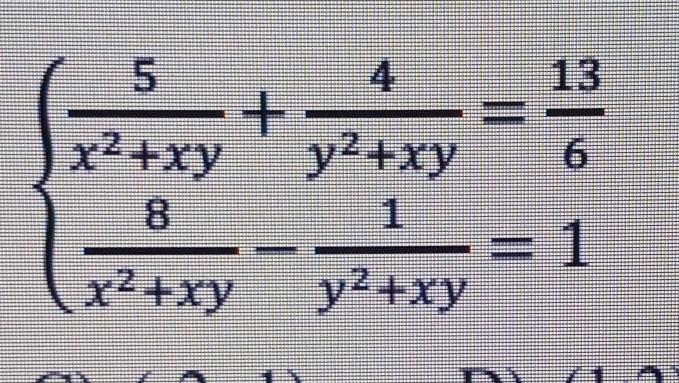
Ответы
Автор ответа:
2
Відповідь:
Пояснення:
Приложения:

dilnura0518:
ohh thanks a lot
Автор ответа:
2
Відповідь:
(2;1) & (-2;-1)
Пояснення:
Похожие вопросы
Предмет: Английский язык,
автор: deryten
Предмет: Окружающий мир,
автор: loymurs
Предмет: Русский язык,
автор: dawa1006
Предмет: Русский язык,
автор: Аноним