Предмет: Математика,
автор: Prostoviiiii
будь ласка, потрібна допомога
Приложения:

Ответы
Автор ответа:
1
Ответ:
А) [-8;0]
Пошаговое объяснение:
Рассмотрим 2 случая:
а) Если х+4 < 0, тогда
б) Если х+4 ≥ 0, тогда
Объединяя оба случая, получится решение x∈[-8;0]
Автор ответа:
1
Відповідь: [-8;0]
Покрокове пояснення:
Приложения:
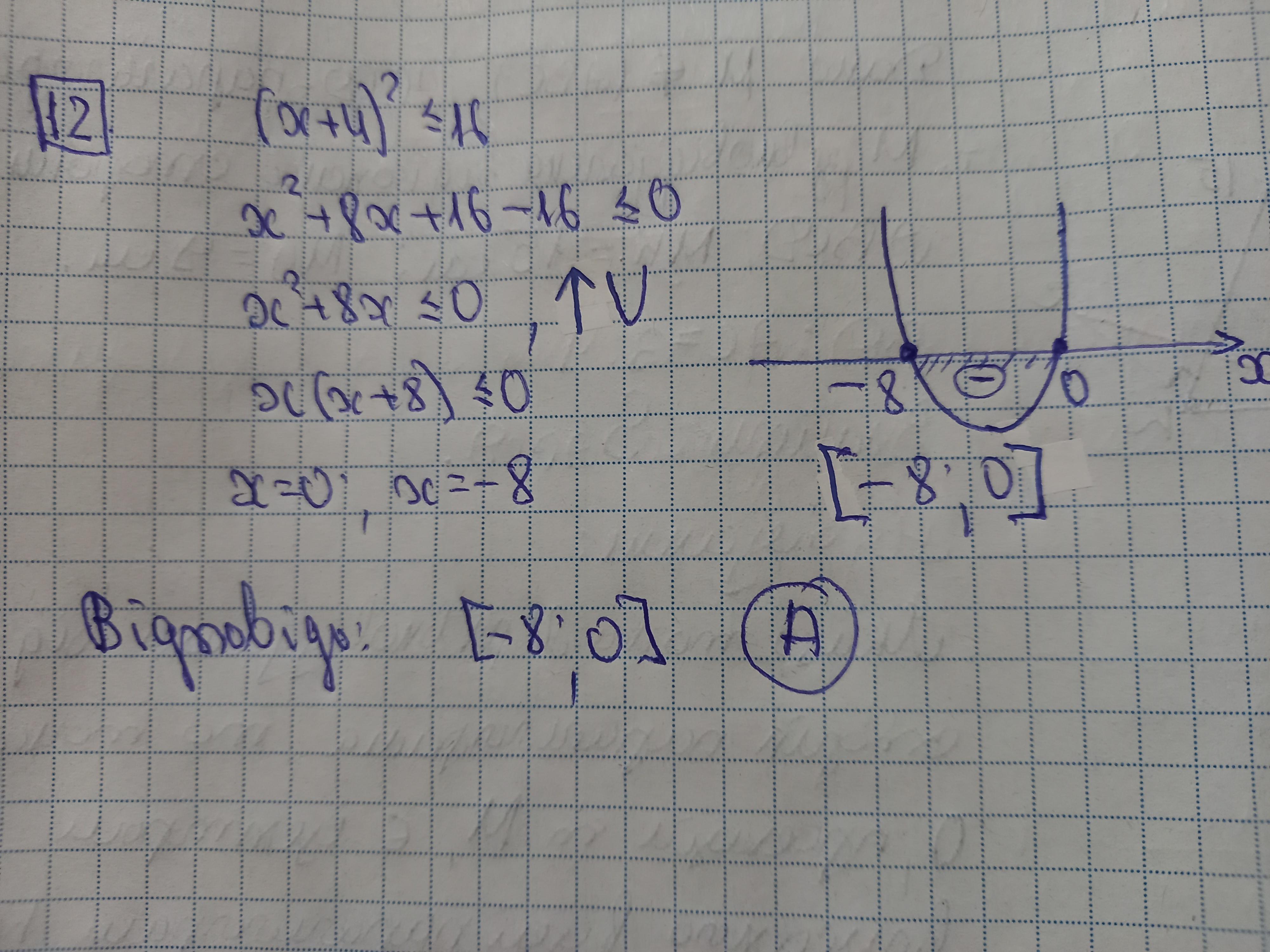
Похожие вопросы
Предмет: Другие предметы,
автор: razumnayatanya
Предмет: Русский язык,
автор: 02101975
Предмет: Русский язык,
автор: Kom18
Предмет: Математика,
автор: sadqboyboy
Предмет: История,
автор: prostomen9826