Предмет: Математика,
автор: Maribe16522
Срочноооо помогите пожалуйста
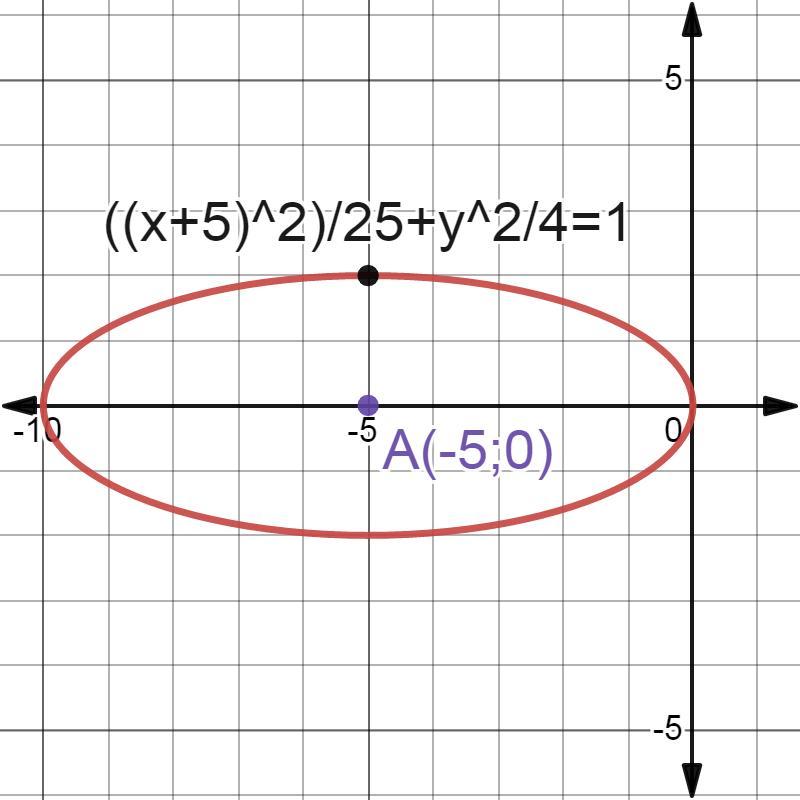
Скласти канонічне рівняння, побудувати еліпс,якщо дано ексцентриситет √21/5 і А(-5;0)
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
каноническое уравнение эллипса имеет вид
х²/а²+у²/b²=1
e=с/а
с=sqrt(a²-b²)
25/a²+0/b²=1
a²=25
e²=(a²-b²)/a²=21/25
(25-b²)/25=21/25
25-b²=21
b²=4
получаем каноническое уравнение эллипса
х²/25+y²/4=1
Автор ответа:
0
Пошаговое объяснение:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: stabina
Предмет: Английский язык,
автор: катярошка
Предмет: Русский язык,
автор: Анна114678888
Предмет: Геометрия,
автор: 2000nic
Предмет: Русский язык,
автор: alim4885