Question

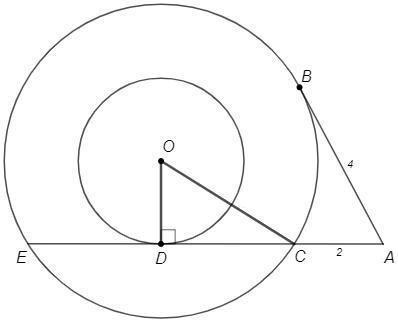
Точка О является центром окружности. D — точка касания. Найдите заштрихованную площадь, если:
AB = 4, AC = 2

Answer 1

Ответ:

Сначала поясним, что площадь закрашенной части ( "кольца") можно найти отняв от площади большего площадь меньшего.

Квадрат касательной равен произведению отрезков секущей, проведенной из одной точки.

AB²=AC×AE

4²=2×AE

16=2×AE

AE=8

CE=AE-AC

CE=8-2=6

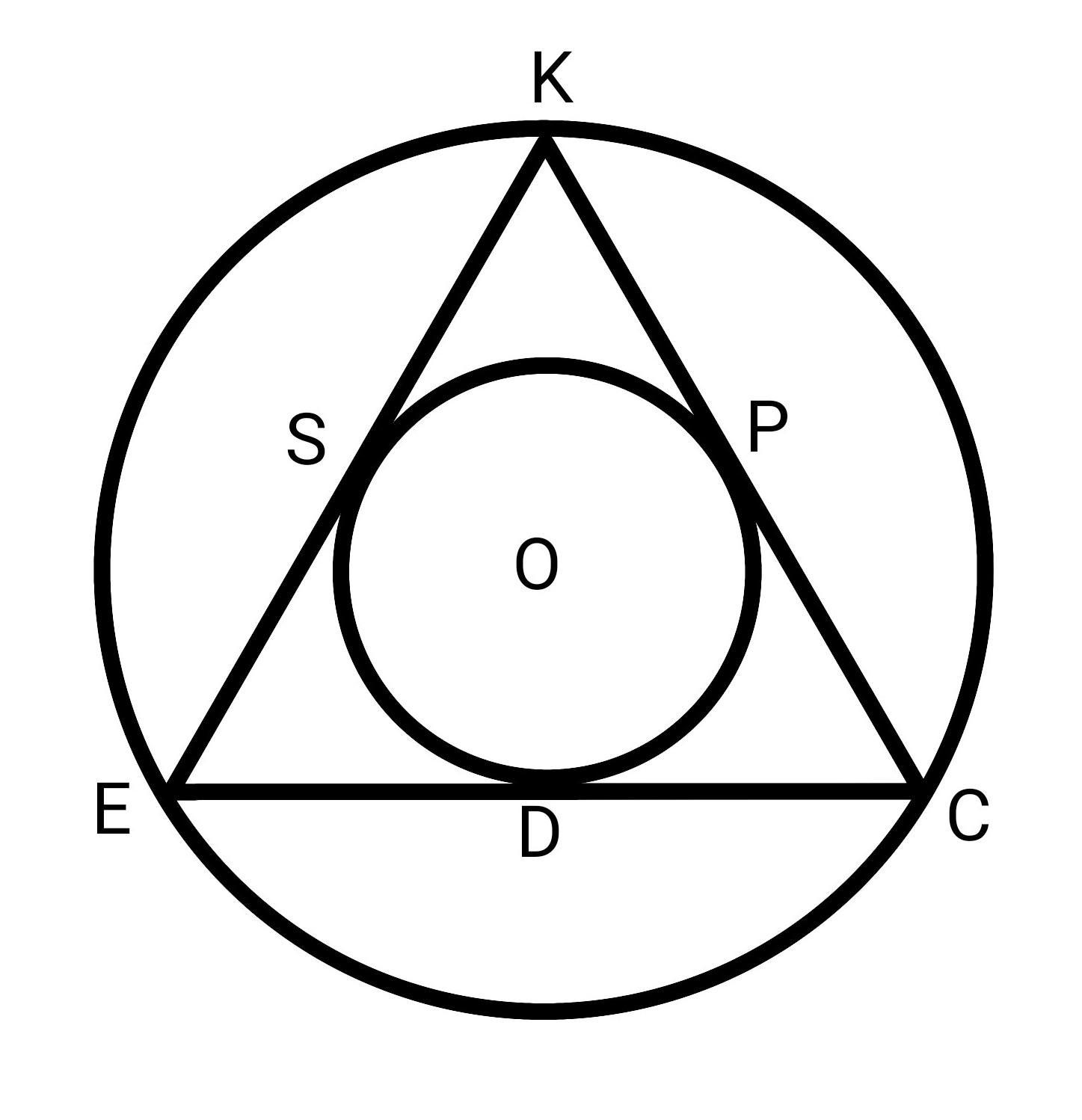
Дочертим треугольник, как на рисунке, где CE=CK=EK=6.

Получается это равносторонний треугольник, около которого описан круг и в который вписан еще один круг.

Радиус вписанного круга в равносторонний треугольник равняется: $\displaystyle r = \frac{a}{2 \sqrt{3} }$

$\displaystyle r = \frac{6}{2 \sqrt{3} } = \sqrt{3}$

Радиус описанного круга около правильного треугольника равняется: $\displaystyle R = \frac{a}{ \sqrt{3} }$

$\displaystyle R = \frac{6}{ \sqrt{3}} = 2\sqrt{3}$

Площадь круга: $S = \pi { r }^{2}$

$S_{1} = \pi \times { \sqrt{3} }^{2} = 3\pi$

$S_{2} = \pi \times {(2 \sqrt{3} )}^{2} = 12\pi$

Площадь заштрихованной части

$S_{2} - S_{1} = 12\pi - 3\pi = 9\pi$

Ответ: 9π кв. ед.

Answer 2

По теореме о касательной и секущей

AB^2 =AE*AC => AE=16/2=8

CE=8-2=6

Радиус в точку касания перпендикулярен касательной, OD⊥CE

Перпендикуляр из центра к хорде делит ее пополам, CD=CE/2=3

OC^2-OD^2 =CD^2 =9 (△OCD, т Пифагора)

Искомая площадь пOC^2 -пOD^2 =п(OC^2-OD^2) =9п