Предмет: Алгебра,
автор: ifeelsobad
Помогите, пожалуйста, решить уравнение
Приложения:
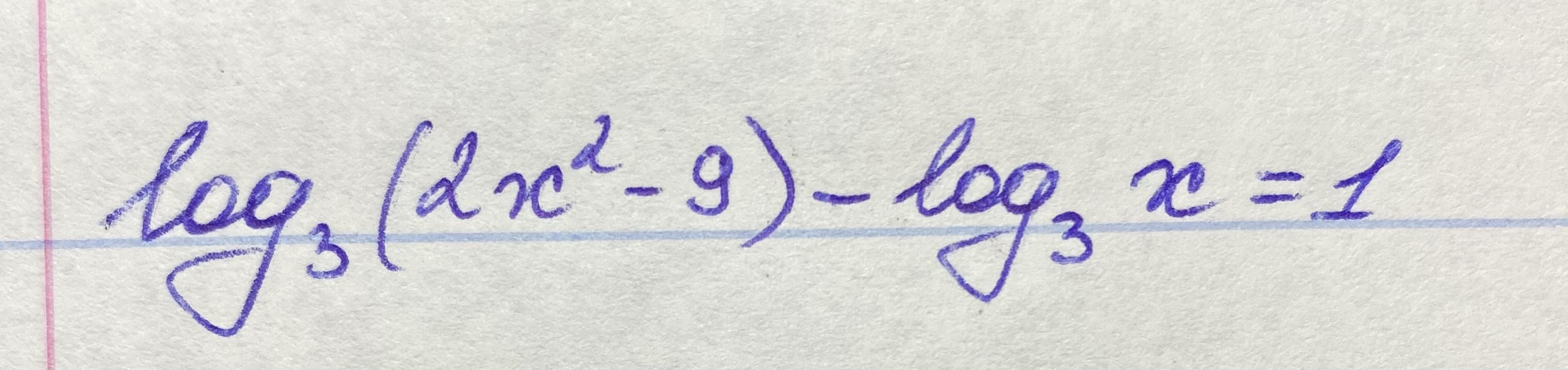
Ответы
Автор ответа:
2
Ответ:
х = 3
Объяснение:
ОДЗ:
По Т. Виетта:
Следовательно можно разбить на множители
С учетом ОДЗ:
Ответ: х = 3
bb573878:
поправьте https://prnt.sc/fXGIQv_4pXrL
Имеется в виду самая верхняя моя строчка?
ага
Да, спасибо - не заметил:)
Похожие вопросы
Предмет: Английский язык,
автор: Jeanne111
Предмет: Русский язык,
автор: мфд251828
Предмет: Русский язык,
автор: lizukash
Предмет: Химия,
автор: sergey0372
Предмет: Математика,
автор: iulia676