Question

Помогите пожалуйста срочно

Answer 1

Ответ:

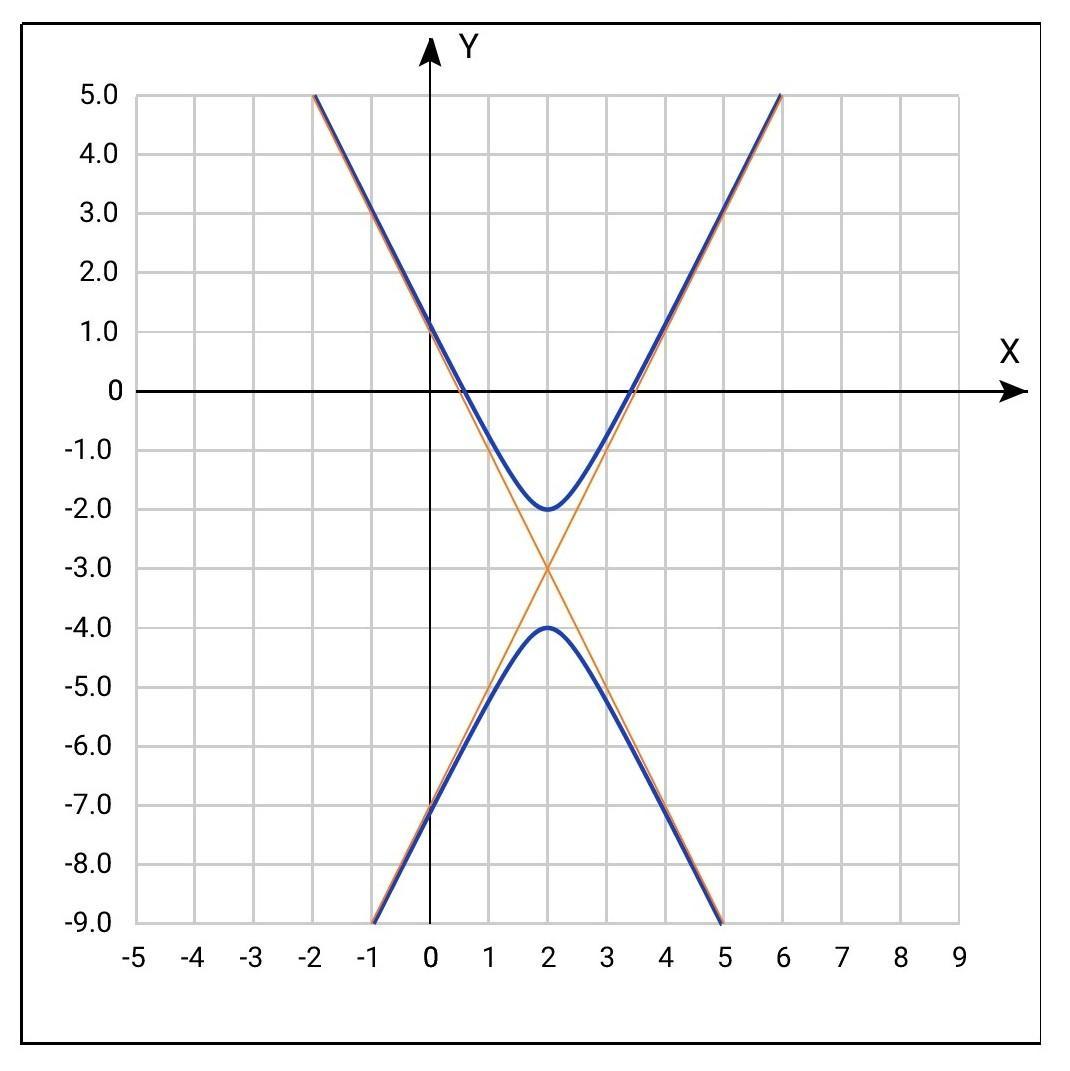
График функции - гипербола.

Каноническое уравнение

$\small - \frac{ {(x - 2)}^{2} }{ {1}^{2} } + \frac{ {(y + 3)}^{2} }{ {2}^{2} } = 1$

Координаты вершин фокусов:

$\small \: F_1(2; \: - 3{-} \sqrt{5} ); \: \small \:F_2(2; \: - 3{+} \sqrt{5} ).$

Ассимптоты:

$y = 1 - 2x ; \\ y = 2x - 7.$

График - см. на приложенном рисунке

Пошаговое объяснение:

$4x^2-y^2-16x-6y+11=0 \\ 4 {x}^{2} - 16x + 16 - ( {y}^{2} + 6y + 9) + 4 = 0 \\ 4 ({x}^{2} - 4x + 4)- ( {y}^{2} + 6y + 9) + 4 = 0 \\ \small 4(x - 2)^{2} - (y + 3)^{2} + 4 = 0 \: \: \: \: \bigg| { \times} \big({ - } \large\tfrac{1}{4} \small \big) \\ \small - \frac{ {(x - 2)}^{2} }{1} + \frac{ {(y + 3)}^{2} }{4} - 1 = 0 \\ \small - \frac{ {(x - 2)}^{2} }{1} + \frac{ {(y + 3)}^{2} }{4} = 1\\ \small - \frac{ {(x - 2)}^{2} }{ {1}^{2} } + \frac{ {(y - ( - 3))}^{2} }{ {2}^{2} } = 1$

Это - уравнение гиперболы, вида:

$- \frac{(x - x_{0})}{{a}^{2} } + \frac{(y - y_{0})}{{b}^{2} } = 1 \\ x_{0} = 2;\;y_{0} = - 3;\;a = 1;\;b = 2$

Фокусы данной гиперболы расположены вдоль оси Оу.

Координаты центра гиперболы: О(2; -3)

Фокусное расстояние - величина 2с, где

$c = \sqrt{ {a}^{2} + {b}^{2} }$

Вычислим

$c = \sqrt{ {1}^{2} + {2}^{2} } = \sqrt{5 \: }$

Вычислим фокусы гиперболы.

Так как они расположены вдоль Оу,

то их координаты будут такими:

$F_1=F_1(x_0; \: y_0{-}c);\\ F_2=F_2(x_0; \: y_0{+}c).$

Вычисляем:

$F_1=F_1(2; \: - 3{-} \sqrt{5} );\\ F_2=F_2(2; \: - 3{+} \sqrt{5} ).$

Найдем ассимптоты. Для этого приравняем левую часть канонического уравнения к 0:

$\small - \frac{ {(x - 2)}^{2} }{ {1}^{2} } + \frac{ {(y + 3)}^{2} }{ {2}^{2} } = 0 \\ \small \frac{ {(y + 3)}^{2} }{ {2}^{2} }- \frac{ {(x - 2)}^{2} }{ {1}^{2} } = 0 \\ \small (y + 3)^{2} - 4(x - 2)^{2} = 0 \\ (y + 3 + 2(x - 2))(y + 3 - 2(x - 2)) = 0 \\ (y + 2x - 1)(y - 2x + 7) = 0 \: \\ \small\begin{cases} y + 2x - 1 = 0 \\ y - 2x + 7 = 0 \end{cases}{ < = > }\begin{cases} y = 1 - 2x \\ y = 2x - 7 \end{cases}$

Уравнения получившейся системы - и являются уравнениями графиков ассимптот нашей гиперболы.