Question

Вычислите площадь фигуры, ограниченой линией y=3x+6,y=0,x=1.
Помогите пожалуйста, срочно!

Answer 1

Ответ:

S = 13.5 кв.ед

Пошаговое объяснение:

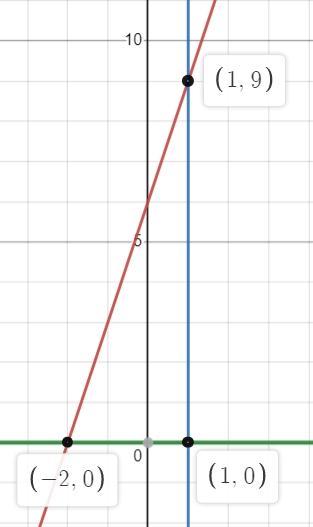
Прежде всего рисуем график.

Оно, конечно, можно и интеграл посчитать.

$\displaystyle S=\int\limits^1_{-2} {(3x+6)} \, dx =\frac{3x^2}{2} \bigg|_{-2}^1+6x\bigg|_{-2}^1=-\frac{9}{2} +18=\frac{27}{2} =13.5$  (кв. ед.)

А можно сразу по графику (не зря ж мы его строили) увидеть, что это прямоугольный треугольник с катетами 3 и 9, поэтому его площадь

$\displaystyle S= \frac{3*9}{2} =13.5$ (кв. ед.)