Предмет: Математика,
автор: ivannavel80
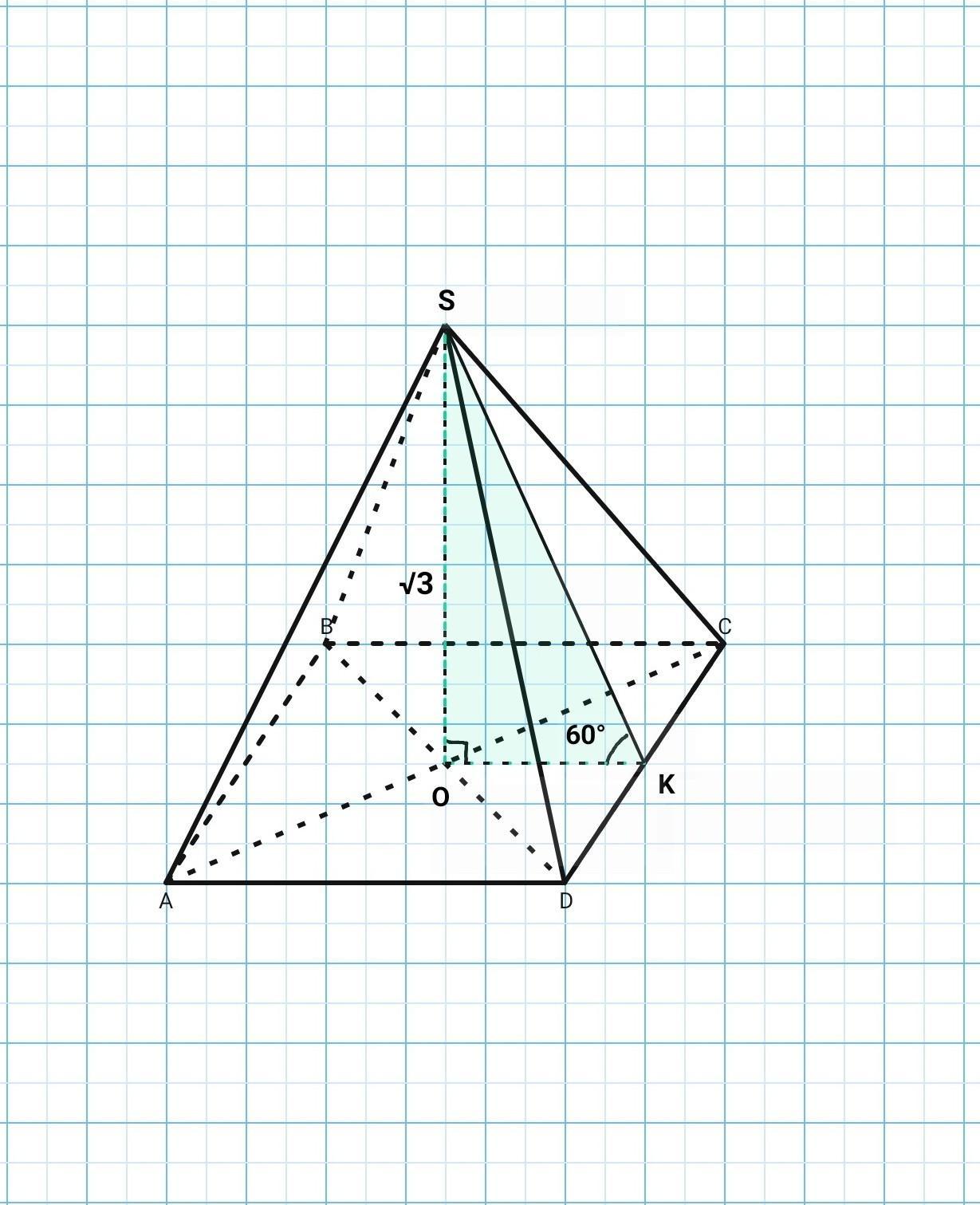
Висота правильної чотирикутної піраміди дорівнює √3 см, апофема нахилена до площини основи під кутом 60°. Знайти повну площу поверхні цієї піраміди. Подскажите пожалуйста
Ответы
Автор ответа:
1
Ответ:
Sп=12см²
Пошаговое объяснение:
- Правильная четырёхугольная пирамида - это пирамида, в основании которой лежит правильный четырёхугольник (в данном случае это квадрат), а боковые рёбра являются равнобедренным треугольниками.
- Площадь полной поверхности пирамиды: Sп = Sосн + Sб
Для решения задачи нам необходимо найти сторону основания (квадрата) и апофему SK.
Рассмотрим прямоугольный треугольник SKO(∠O=90°).
SK= 2 см
∠OSK=90°-∠SKO=90°-60°= 30°
В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы:
ОК =½•SK=½•2= 1 см
DC= AD=BC=AB =2• OK=2•1 = 2 см
Тогда Sосн=а²=DC²=2²= 4 см².
Sб=4•S(△DSC)=4•½•DC•SK=2•2•2= 8 см²
Sп = 4+8 = 12 см²
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: liza2444
Предмет: Русский язык,
автор: Муниша
Предмет: Английский язык,
автор: nagibators222
Предмет: Алгебра,
автор: shura818
Предмет: Алгебра,
автор: tru55