Question

Сторона ромба дорівнює 15 см, а одна з діагоналей 18 см.Обчислити довжину іншої діагоналі.​

Answer 1

Ответ:

Вторая диагональ равна 24 см.

Пошаговое объяснение:

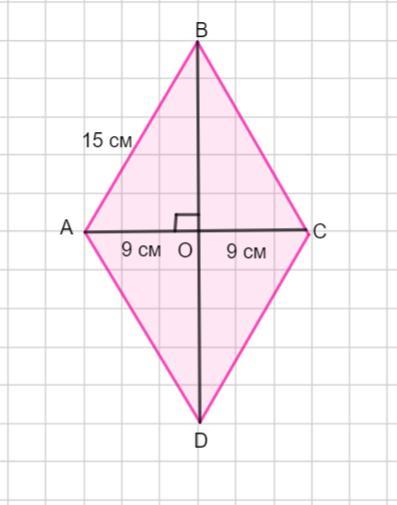
Пусть дан ромб АВСD .

У ромба все стороны равны АВ =ВС =СD=АD =15 см .

Диагональ АС =18 см. Надо найти диагональ ВD.

Диагонали ромба пересекаются в тоске О и точкой пересечения делятся пополам. Значит, АО =ОС =18 : 2 =9 см.

Диагонали ромба пересекаются под прямым углом.

Тогда Δ АОВ - прямоугольный.

Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB^{2} =AO^{2} +BO^{2} ;\\BO^{2} =AB^{2} -AO^{2};\\BO= \sqrt{AB^{2} -AO^{2}} ;\\BO= \sqrt{15^{2}-9^{2} } =\sqrt{(15-9)(15+9)} =\sqrt{6\cdot24} =\sqrt{6\cdot6\cdot 4} =6\cdot2=12$ см.

Тогда диагональ будет равна

$BD=2\cdot BO;\\BD =2\cdot 12 =24$ см.