Предмет: Алгебра,
автор: masha01021
помогите пожалуйста решить задачу по алгебре
Приложения:

Ответы
Автор ответа:
0
Ответ:
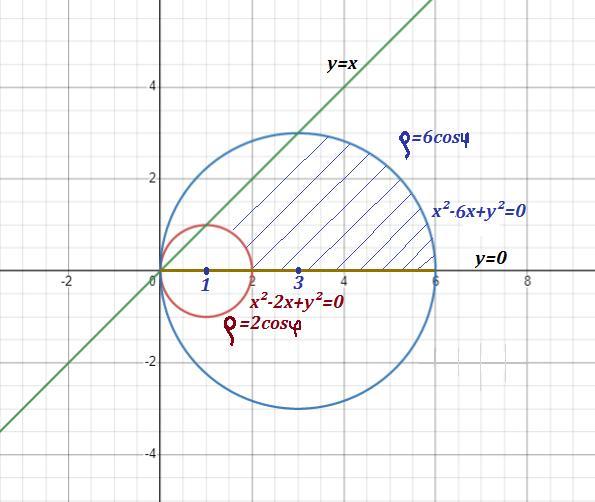
- окружность с центром в точке (1;0) и радиуса R=1 .
В полярных координатах запишем это уравнение, заменив
.
Аналогично , - это окружность с
центром в точке (3;0) и радиуса R=3 . В полярных координатах это
уравнение будет иметь вид: .
y=x - это прямая, биссектриса 1 и 3 координатных углов ,
y=0 - это ось ОХ ,
Площадь области в полярной системе координат вычисляется по
формуле
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Азяка21
Предмет: Английский язык,
автор: Tabyash
Предмет: Русский язык,
автор: али410
Предмет: Алгебра,
автор: sidenko762
Предмет: Математика,
автор: cebura33