Question

Здравствуйте помогите пожалуйста

Answer 1

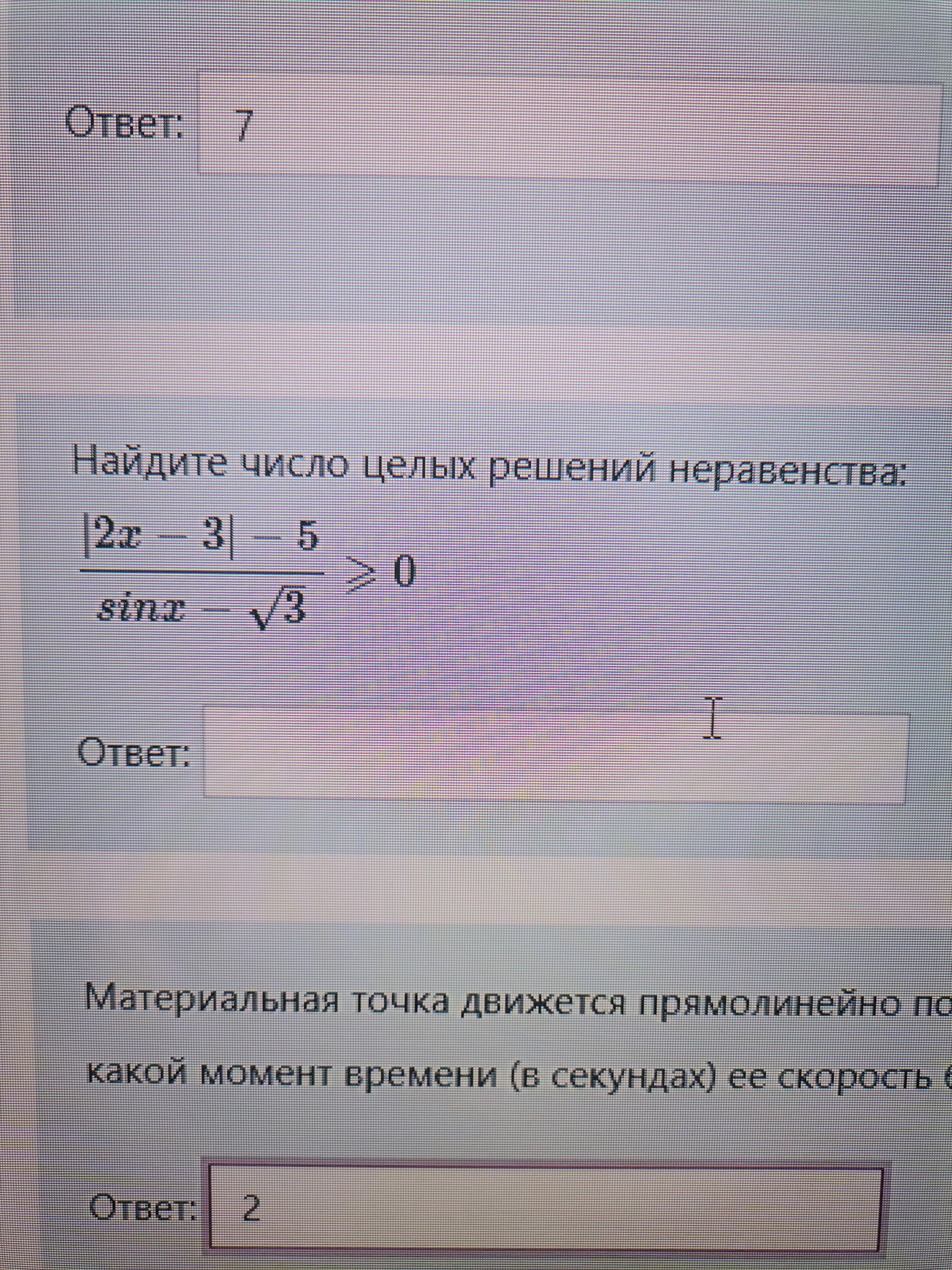
Ответ:

целых решений 6

Пошаговое объяснение:

$\displaystyle \frac{|2x-3|-5x}{sin(x)-\sqrt{3} } \geq 0$

В данном выражении знаменатель всегда меньше 0.

(sin(x) ≤ 1;  √3 ≈ 1,7320)

Поэтому нам надо рассмотреть неравенство

|2x-5| -5 ≤ 0

$\displaystyle \left \{ {{2x-3\leq 5} \atop {2x-3\geq -5}} \right. \left \{ {{2x\leq 8} \atop {2x\geq -2}} \right. \left \{ {{x\leq 4} \atop {x\geq -1}} \right. \Rightarrow x\in[-1;\;4]$

Теперь посчитаем целые решения

-1; 0; 1; 2; 3; 4

Их всего 6.

#SPJ1