помогите пж с задачей геометрия 10 класс
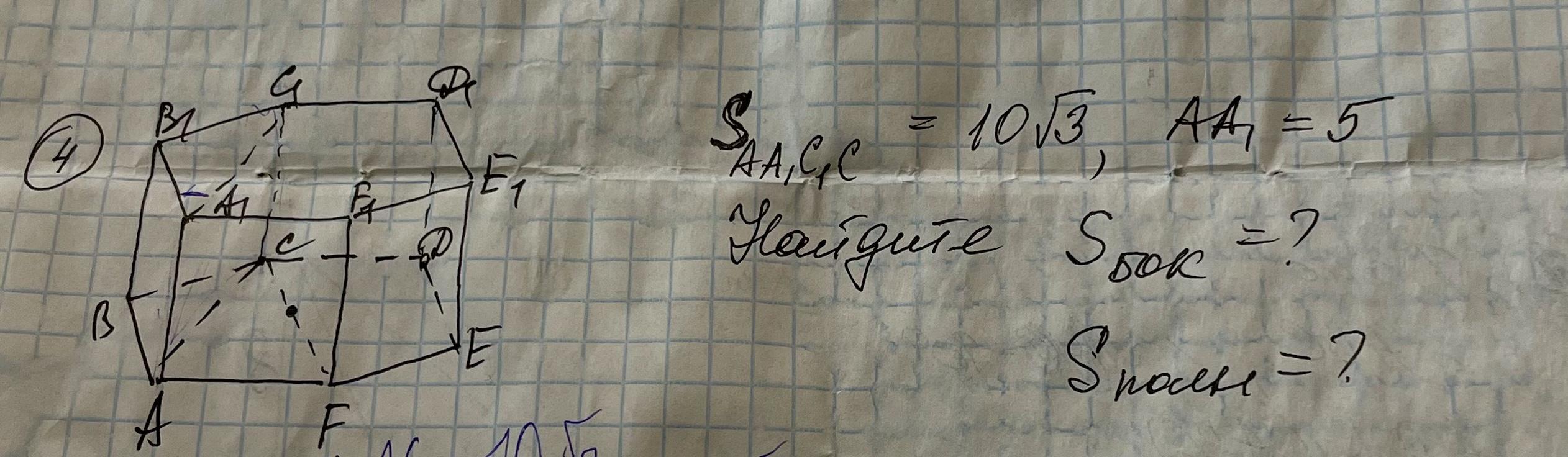
Ответы
Ответ:
Площадь боковой поверхности равна 60 кв.ед., а площадь полной поверхности равна (60+12 √3) кв. ед.
Объяснение:
По условию задана правильная шестиугольная призма.
Надо найти площадь боковой поверхности призмы и площадь полной поверхности призмы.
Площадь боковой поверхности призмы найдем как произведение периметра основания на высоту призмы.
Высота призмы равна боковому ребру и равна 5 ед.
Четырехугольник прямоугольник. Площадь прямоугольника равна произведению длины на ширину.
Тогда
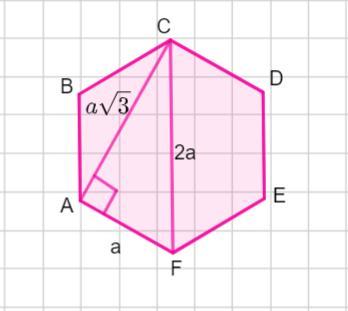
Рассмотрим правильный шестиугольник ( рисунок во вложении ) АС - меньшая диагональ шестиугольника . Если сторона шестиугольника а, большая диагональ шестиугольника 2а. Тогда найдем меньшую диагональ по теореме Пифагора
Значит, сторона правильного шестиугольника
Тогда периметр шестиугольника
ед.
И площадь боковой поверхности будет равна
кв. ед.
Площадь полной поверхности равна сумме площади боковой поверхности и удвоенной площади основания.
Найдем площадь правильного шестиугольника по формуле
где а -сторона шестиугольника
кв. ед.
Тогда площадь полной поверхности
кв. ед.
#SPJ1