Question

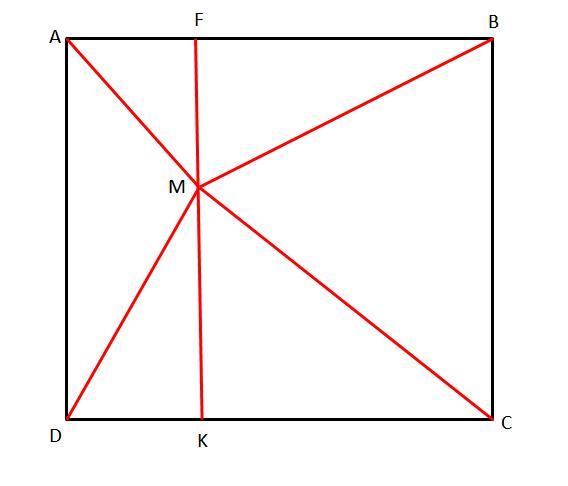
Точка М лежит внутри квадрат ABCD так что ∠MAB = 60°
∠MCD = 15°. Нaйти угол MBC

Answer 1

Ответ:

Пусть сторона квадрата будет _ а  (AB = BC= CD = DA = a)

MF⊥AB, MK⊥CD

AD = BC = MK + MF

AB = CD = CK + AF

 =>

MK + MF = KC + AF = a

∠MAB = ∠MAF

∠MCD = ∠MCK

=>

∠MAF = 60°

∠MCK = 15°

ИЗ прям треугольника АMF

AF = AM · cos∠MAF

FM = AM ·sin∠MAF

Из прям. треугольника CMK

KC = MC · cos∠MCK

MK = MC · sin∠MCK

=>

AM · sin∠MAF + MC · sin∠MCK = a

поскольку АF = AM · cos∠MAF, KC = MC · cos∠MCK,  KC + AF = a

=>

$\left \{ {{AM ^{.} sin < MAF + MC ^{.} sin < MCK = a} \atop {AM ^{.} cos < MAF + MC ^{.} cos < MCK = a}} \right.$

$\frac{MA ^{.} cos < MAB }{cos < MCK} - \frac{MA ^{.} sin < MAB}{sin < MCK} = \frac{a}{cos < MCK} = \frac{a}{sin < MCK}$

(умнож.) sin∠MCK · cos∠MCK  

MA · (cos∠MAB · sin∠MCK - sin∠MAB · cos∠MCK) = a (sin∠MCK - cos∠MCK)

MA · sin (∠MAB - ∠MCK) = a · (cos∠MCK - sin∠MCK)

MA · sin (∠MAB - ∠MCK) = a$\sqrt{2}$ · (sin45° · cos∠MCK - cos45° · sin∠MCK)

sin (45° - ∠MCK) = a√2 ·sin (45° - ∠MCK) =>

MA · sin (60° - 15°) = a√2 · sin ( 45° - 15° )

sin ( 60° - 15° ) = sin 45° = √2/2

sin ( 45° -15° ) = sin 30° = 1/2

=>

MA · $\frac{\sqrt{2} }{2}$ = a√2 · $\frac{1}{2}$

MA = a

поскольку треугольник  МАВ равнобедренный то есть МА = а

=>

∠AMB = ∠ABM

так как сумма внутренних углов всех треугольников равна 180°

∠AMB + ∠ABM + ∠MAB = 180°

=>

∠AMB = ∠ABM = $\frac{180^{0} - < MAB}{2} = \frac{120^{0} }{2} =60^{0}$

∠MBC = ∠B - ∠ABM

=>

∠MBC = 90° - 60° = 30°