Question

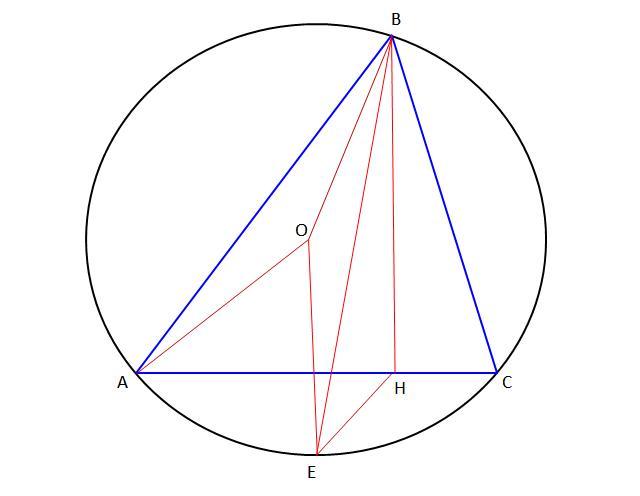
Из вершины B треугольника ABC проведена высота BH и биссектриса_которая пересекает окружность, описанную треугольником, в точке E. Докажите, что BE — середина угла OBH

Answer 1

Ответ:

( О центр окружности )

Поскольку ВЕ биссектриса угла АВС

∠ABE = ∠CBE = $\frac{ < ABC}{2}$

Поскольку ВH высота

∠BHC = 90°

из равнобедренного треугольника АОВ

центральный угол АОВ равен дуги АВ

так как сумма внутренних углов всех треугольников равна 180°

а в треугольнике АОВ

∠ОАВ = ∠ОВА  =>

∠ОАВ = ∠ОВА = $\frac{180^{0} - < AOB }{2}$ = $\frac{180^{0} - AB }{2}$

Вписанный угол АСВ равен половине дуги АВ

∠АСВ = $\frac{AB}{2}$

∠HCB = ∠ACB    =>

∠HCB = $\frac{AB}{2}$

так как сумма внутренних углов всех треугольников равна 180°

⇒

из треугольника HСВ

∠BHC + ∠HCB +∠HBC = 180° =>

∠HBC = 180° - (∠BHC + ∠HCB) = 180° - (90° + $\frac{AB}{2}$) = $\frac{180^{0}-AB }{2}$$\frac{180^{0}-AB }{2}$

значит получается что

∠ОВА = ∠HBC = $\frac{180^{0}-AB }{2}$

∠ABE = ∠OBA + ∠OBE,   ∠CBE = ∠HBC + ∠HBE

=>

∠OBE = ∠ABE - ∠OBA,   ∠HBE = ∠CBE - ∠HBC

поскольку ∠ABE = ∠CBE = ∠ABC / 2,  ∠OBA = ∠HBC = 180°- AB / 2

получается что

∠OBE = ∠HBE = ∠ABC / 2 - 180° - AB / 2

так как ∠ОBE = ∠HBE   =>  BE биссектриса угла OBH

Answer 2

∠ABH=90°-A

∠BOC =◡BC =2A

△BOC -р/б (OB=OC)

∠OBC=(180°-∠BOC)/2 =(180°-2A)/2 =90°-A

∠ABH =90°-A =∠OBC

∠HBE =∠ABE-∠ABH =∠CBE-∠OBC =∠OBE

=> BE - биссектриса ∠OBH