Предмет: Геометрия,
автор: koopleasethanks
СРОЧНО ДАЮ 30 БАЛЛОВ!
Через вершину В прямокутника АВСD проведено пряму МВ, перпендикулярну до сторін прямокутника АВ і ВС. Доведіть перпендикулярність площин МСD і площини МВС.
Відповідь з малюнком!
BMW52:
Обязательно с рисунком?
да
Ответы
Автор ответа:
1
Ответ:
Доказано, что MCD ⊥ MBC.
Объяснение:
Через вершину прямоугольника АВСD проведена прямая МВ, перпендикулярная к сторонам прямоугольника АВ и ВС. Докажите перпендикулярность плоскостей МСD и плоскости МВD.
Дано: АВСD - прямоугольник;
МВ ⊥ АВ; МВ ⊥ ВС;
Доказать: MCD ⊥ MBC.
Доказательство:
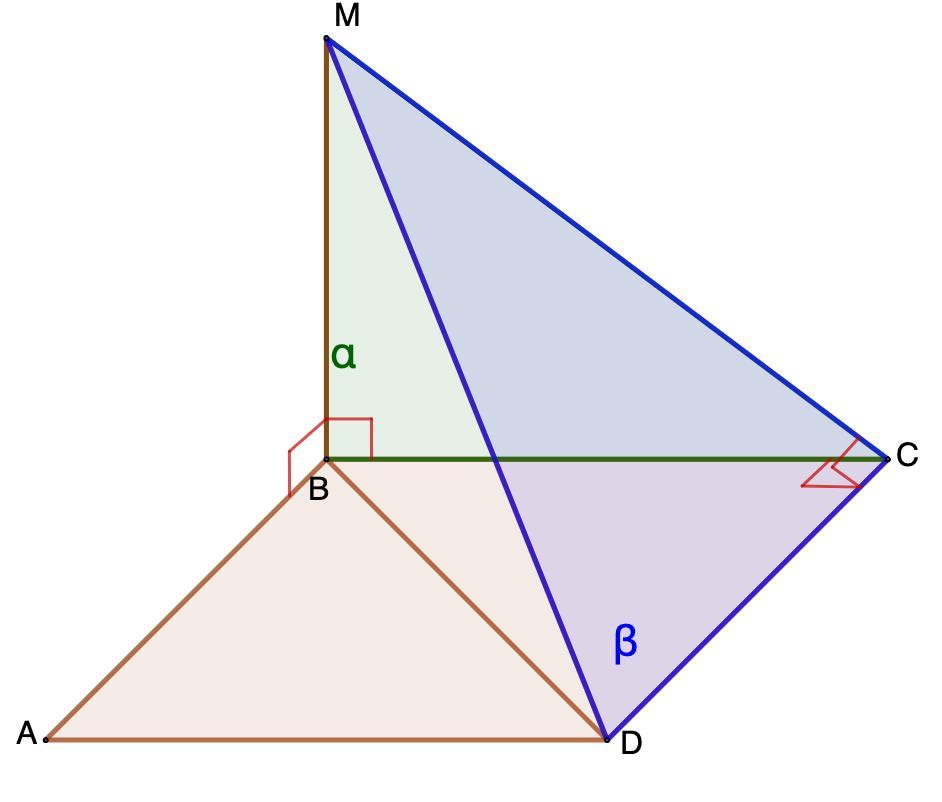
Пусть плоскость MBC - α; плоскость MCD - β.
МВ ⊥ АВ; МВ ⊥ ВС (условие);
АВ ∩ ВС = В.
- Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
⇒ МВ ⊥ ABCD.
MC - наклонная.
⇒ ВС - проекция МС на плоскость ABCD.
BC ⊥ DC (АВСD - прямоугольник)
- Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
⇒ MC ⊥ DC.
MC ∩ BC = C; DC ⊥ MC; DC ⊥ BC
⇒ DC ⊥ α.
DC ⊂ β
- Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
⇒ α ⊥ β или MCD ⊥ MBC.
Доказано, что MCD ⊥ MBC.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: евачка2004
Предмет: Окружающий мир,
автор: Sonyanumber1
Предмет: Українська мова,
автор: maks22813372
Предмет: Алгебра,
автор: praxegor
Предмет: История,
автор: marysya87385