Предмет: Математика,
автор: igonovedir
составить уравнение касательной к графику функции F от X в точке X0
Приложения:
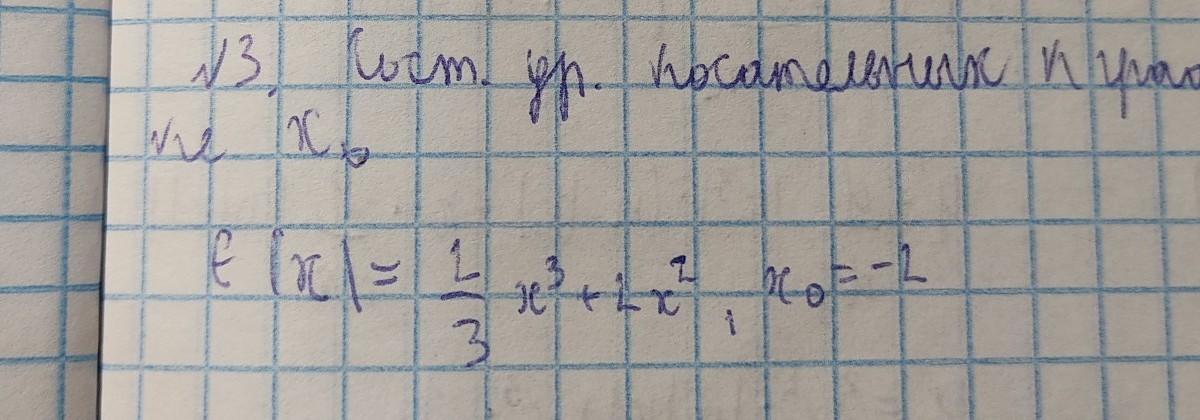
Ответы
Автор ответа:
1
Ответ:
Уравнение касательной:
igonovedir:
там не 1/3, а 1/2
Похожие вопросы
Предмет: Французский язык,
автор: ahhashishkina22
Предмет: Русский язык,
автор: Tinalok
Предмет: Русский язык,
автор: Almighty74
Предмет: Химия,
автор: miracocs
Предмет: Геометрия,
автор: VladvTanke