Помогите решить систему уравнений
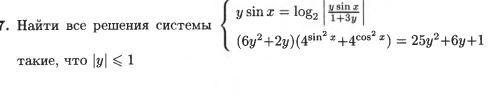
Ответы
Ответ:
(см. объяснение)
Пошаговое объяснение:
Заметим, что при любом
принимает значения от
до
.
Тогда верно, что:
Из второй строки исходной системы следует:
Тогда получим:
Решаем это двойное неравенство:
По условию задачи , то есть
.
Тогда рассматриваем только следующие :
Рассмотрим сначала самый простой случай, когда .
Тогда исходная система примет вид:
Решение обоих уравнений очевидно и потому опускается.
Отметим только, что в результате получатся пары чисел , которые удовлетворяют исходной системе.
Рассмотрим теперь промежуток .
Обратимся к первой строке исходной системы:
Заметим, что так как и
, то верна оценка
.
По первой строке системы можно сделать подстановку:
Уйдем от логарифма:
Заметим, что при верно
, то есть
не превосходит единицы. Но и синус лежит в диапазоне от
до
.
То есть дробь на условии задачи будет всегда меньше
.
Поэтому можно написать просто:
Умножаем обе части неравенства на :
Дробь не превосходит единицы на условии задачи. Ситуация с синусом аналогичная. Тогда значение большее единицы мы гарантированно получить не можем.
Значит осталось проверить в ручную:
Что есть следующее:
Это аргумент логарифма, тогда удобно обратиться к первой строке исходной системы:
Поскольку , то равенство теоретически возможно только, если окажется, что
и
.
Однако очевидно, что это не решения системы.
Поэтому при исходная система уравнений имеет решения:
Система уравнений решена!