Question

ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА
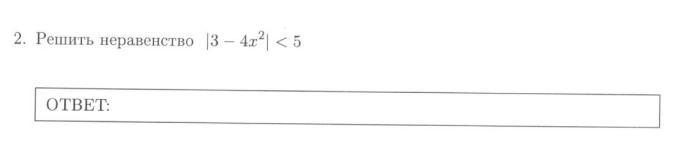
решите неравенство 3-4x^2<5

Answer 1

Ответ:

x∈ (-√2;√2)

Пошаговое объяснение:

|3-4x²| < 5
Рассмотрим 2 случая:
1) Если 3-4x² < 0:
$\displaystyle \left \{ {{3-4x^2 < 0} \atop {-(3-4x^2) < 5}} \right. < = > \left \{ {{4x^2 > 3|:4} \atop {4x^2-3 < 5}} \right. < = > \left \{ {{x^2 > \frac{3}{4} } \atop {4x^2 < 8|:4}} \right. < = > \\ < = > \left \{ {{\left[\begin{array}{ccc}x > \sqrt{3}/2 \\x < -\sqrt{3}/2 \\\end{array}\right. } \atop {x^2 < 2}} \right. < = > \left \{ {{\left[\begin{array}{ccc}x > \sqrt{3}/2 \\x < -\sqrt{3}/2 \\\end{array}\right. } \atop {-\sqrt{2} < x < \sqrt{2} } \right.$
Отсюда x∈ (-√2;-√3/2)U(√3/2;√2)
2) Если 3-4x² ≥ 0:
$\displaystyle \left \{ {{3-4x^2 \geq 0} \atop {3-4x^2 < 5}} \right. < = > \left \{ {{4x^2 \leq 3|:4} \atop {-4x^2 < 2|:(-4)}} \right. < = > \left \{ {{x^2 \leq \frac{3}{4} } \atop {x^2 > -\frac{1}{2} }} \right. < = >$
Решением второго неравенства системы является x∈R, т. к. любое число в квадрате является неотрицательным. Тогда для решения остаётся только первое неравенство
$\displaystyle < = > -\frac{\sqrt{3} }{2} < x < \frac{\sqrt{3} }{2}$

Соединяя решения обоих случаев, получаем, что x∈ (-√2;√2)